18:00 Investigation about 00729 ISG ontology

The 00729 ontology contains 124 full guarded TGDs and 54 non full guarded TGDs, and 33 unguarded full TGDs are discarded for our experiments. So, it is a small ontology.

Surprisingly, GSat requires more than 5 minutes to compute the saturation of this ontology. The ouputted log shows that GSat derived 467 486 non full TGDs and no full TGD. Moreover, the skolemized version of the saturation requires only 2 seconds to complete the saturation, according the logs. Its outputs contains 24 full TGDs that were not contains in the single headed skolemized input TGDs. It appears that Simple Sat is even faster.

In order to understand how GSat behaves on this ontology, I first printed the derived non full TGDs. Unsurprisingly, I discovered that they have large body and head, for example:

uuid70(GSat_u1) & oboTAO_0001428(GSat_u1) & oboBSPO_0000071(GSat_u1) & oboTAO_0002254(GSat_u1) & oboTAO_0001834(GSat_u1) → exists[GSat_e1,GSat_e2] oboBFO_0000053(GSat_e1,GSat_e2) & oboBFO_0000001(GSat_e1) & obo2BSPO_0000071(GSat_e1) & oboBFO_0000050(GSat_e1,GSat_u1) & oboPATO_0000070(GSat_e2) & obo2TAO_0001834(GSat_e1) & oboTAO_0001421(GSat_e1) & oboBFO_0000002(GSat_e1) & oboBFO_0000004(GSat_e1) & oboBFO_0000052(GSat_e2,GSat_e1) & obo3PATO_0000070(GSat_e1) & obo2TAO_0001428(GSat_e1) & oboBFO_0000051(GSat_u1,GSat_e1) & obo2TAO_0002254(GSat_e1)

Then, I thought that the way the TGDs depends from each other was complex enough to derive many TGDs, when evolving. In order to see these dependencies, I drew the rule dependencies graph of the ontology (see Mugnier, Thomazo (2014). An Introduction to Ontology-Based Query Answering with Existential Rules), which is a graph, where nodes are TGDs and there is a edge from r1 to r2 iff we can apply r2 after deriving some facts from an instance using r1. So, I used the tools Kiabora to compute the rule dependencies graph, on which I built a small graph visualization.

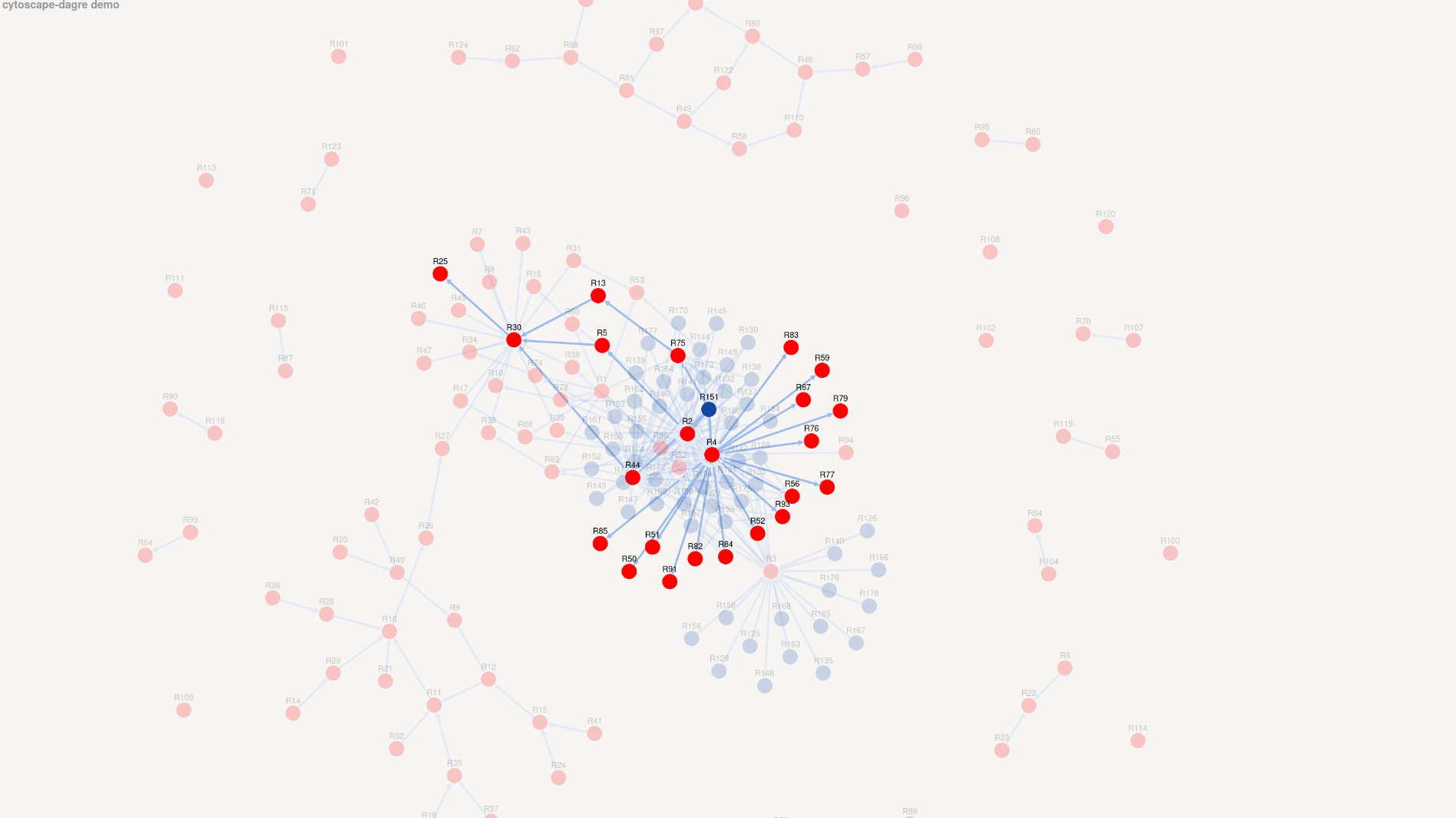
On this picture, you can see the graph, where the red nodes represent the full TGDs and the blue ones the non full TGDs. I discarded the edge which are not useful to understand the behaviour of GSat, i.e. the edges whose target is non full TGDs. We first observe that most of the full TGDs seems not used as an input for evolve, since most of them (red nodes around the group in the centre) are not accessible from a non full TGD (all the blue nodes are in the centre). On the image, you can see all the TGDs accessible from the non full TGD R151, i.e. (need to be proved) all the initial full TGD that may be evolved with R151. I copied these accessible 24 TGDs (see below) into a separate file and ran GSat on them. It tooks almost 1min45s to compile the saturation, which is the set of the initial full TGDs. It did not derived any full TGDs during the execution.

%R2
obo:BFO_0000052(X0, X1) :- obo:BFO_0000053(X1, X0).

%R4
obo:BFO_0000050(X0, X1) :- obo:BFO_0000051(X1, X0).

%R5
obo:BFO_0000004(X0) :- obo:BFO_0000052(X3, X0).

%R13
obo:BFO_0000004(X0) :- obo3:PATO_0000070(X0).

%R25
obo:BFO_0000001(X0) :- obo:BFO_0000002(X0).

%R30
obo:BFO_0000002(X0) :- obo:BFO_0000004(X0).

%R44
obo:BFO_0000004(X0) :- obo:BFO_0000053(X0, X3).

%R50
obo2:TAO_0002254(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0002254(X3).

%R51
obo2:TAO_0001418(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001418(X3).

%R52
obo2:TAO_0001094(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001094(X3).

%R56
obo2:TAO_0000107(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0000107(X3).

%R59
obo2:TAO_0001834(X0) :- obo:TAO_0001834(X3), obo:BFO_0000050(X0, X3).

%R67
obo2:BSPO_0000084(X0) :- obo:BFO_0000050(X0, X3), obo:BSPO_0000084(X3).

%R75
obo3:PATO_0000070(X0) :- obo:BFO_0000053(X0, X3), obo:PATO_0000070(X3).

%R76
obo2:TAO_0001428(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001428(X3).

%R77
obo2:TAO_0001189(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001189(X3).

%R79
obo2:TAO_0000277(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0000277(X3).

%R82
obo2:BSPO_0000071(X0) :- obo:BFO_0000050(X0, X3), obo:BSPO_0000071(X3).

%R83
obo2:TAO_0001421(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001421(X3).

%R84
obo2:TAO_0001238(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0001238(X3).

%R85
obo2:TAO_0000567(X0) :- obo:TAO_0000567(X3), obo:BFO_0000050(X0, X3).

%R91
obo2:TAO_0000519(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0000519(X3).

%R93
obo2:TAO_0000223(X0) :- obo:BFO_0000050(X0, X3), obo:TAO_0000223(X3).

%R151
obo:BFO_0000051(X0, X3), obo:TAO_0001421(X3), obo:BFO_0000053(X3, X4), obo:PATO_0000070(X4) :- uuid:70(X0).

By analysing the set of these TGDs, we see that there is one non full TGD R151 and two kind of full TGDs the linear ones and the others, that have the following form:

B(x, y), C_i(x) -> D_i(y) for i in 1..n

To simplify, we can remove the linear rule and consider that R151 have the following form:

A(x) -> B(x, y)

Applying Evolve of these TGDs will produce the following TGDs, for I a subset of {1…n}:

R_I : A(x), \wedge_{i \in I} C_i(x) -> B(x, y) \wedge_{i \in I} D_i(y)

Since R_I is not subsumed by R_J if I is not equal to J, it means that GSat is creating at least 2ⁿ TGDs.

If we simulate the behaviour of the skolemized version of the saturation on the simple example above, we obtain the following input TGDs:

A(x) -> B(x, f(x))
B(x, y), C_i(x) -> D_i(y) for i in 1..n

It is possible to evolve the first non-full TGD with each of the full TGD to obtain the following non-full TGDs:

A(x) -> C_i(x) -> D_i(f(x)) for i in 1..n

This time, the number of derived TGDs is n.