We used this as the first question in the Maths & CS interview at LMH in December 2020. The question below is from this post. The question is due to Christina Goldschmidt, as is the solution and discussion presented here.

Question:

This question is about the function \(Z\) defined by \( \displaystyle Z(s) = \sum_{k = 1}^\infty \frac{1}{k^s}, \) for \( s > 1 \).

  1. Can you find a lower bound on this function which is valid for all \( s > 1 \)?
  2. Why have we excluded \( s = 1\) from the domain?
From now on, we will concentrate on \( Z(2) \).

  1. Can you find an upper bound on \(Z(2) \)?
In fact, \( \displaystyle Z(2) = \frac{\pi^2}{6} \), i.e., \( \displaystyle \sum_{k=1}^n \frac{1}{k^2} \rightarrow \frac{\pi^2}{6} \) as \( n \rightarrow \infty \).

  1. One proof of this fact relies on the inequalities
    \( \sin \theta < \theta < \tan \theta,~~~~\)for \(\theta \in (0, \pi/2)\).
    Can you show why this is true geometrically?
  2. Can you use this to get upper and lower bounds on \(1/\theta^2\) in terms only of \(\tan \theta\)?
  3. Now let \( \theta_k = \frac{k \pi}{2 n + 1} \) for \(1 \leq k \leq n \). Find upper and lower bounds on \[ \sum_{k=1}^n \frac{1}{k^2}. \]
  4. It turns out that the numbers \[ r_k = \frac{1}{\tan^2 \left( \frac{\pi k}{2n + 1 } \right) }, ~~ 1 \leq k \leq n, \] are roots of the polynomial \[ p_n(x) = { 2n + 1 \choose 1} x^n - {2n + 1 \choose 3} x^{n-1} + \cdots + (-1)^n {2n + 1 \choose 2n + 1}. \] Can you use this to show that
    \( \displaystyle \sum_{k=1}^n \frac{1}{k^2} \rightarrow \frac{\pi^2}{6} \) as \( n \rightarrow \infty \)?

Solution:

  1. The first term in the sum is \(1\) and the others are all strictly positive, so \(Z(s) \gt 1\) for all \(s \gt 1\).

  2. Because the sum in that case is infinite. Note that the sum of the first \(n\) terms is the \(n\)th harmonic number \(H_n\) and \(H_n \sim \log n\) as \(n \) gets large. Since \(\log n \rightarrow \infty \) as \( n \rightarrow \infty\), we have \(H_n \rightarrow \infty\).

    In order to prove this, note that \[ \sum_{k=1}^n \frac{1}{k} \geq \int_{1}^{n+1} \frac{1}{x} dx = \log(n + 1). \]

    Alternatively, \begin{align*} &1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \cdots\\ \geq& 1 + \frac{1}{2} + \underbrace{\frac{1}{4} + \frac{1}{4}}_{2} + \underbrace{\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}}_{4} + \underbrace{\frac{1}{16} + \cdots + \frac{1}{16}}_{8} + \cdots \\ =&1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots = \infty. \end{align*}

  3. \(Z(2) \leq 2\). In order to see this, note that \[ \sum_{k=1}^\infty \frac{1}{k^2} \leq 1 + \sum_{k=2}^\infty \frac{1}{k (k-1)} = 1 + \sum_{k=2}^\infty \left( \frac{1}{k-1} - \frac{1}{k} \right) = 2,\] since the sum telescopes. Alternatively, \begin{align*} &1 + \underbrace{\frac{1}{2^2} + \frac{1}{3^2}}_{} + \underbrace{\frac{1}{4^2} + \frac{1}{5^2} + \frac{1}{6^2} + \frac{1}{7^2}}_{} + \frac{1}{8^2} + \cdots\\ \leq& 1 + \underbrace{\frac{1}{2^2} + \frac{1}{2^2}}_{2} + \underbrace{\frac{1}{4^2} + \frac{1}{4^2} + \frac{1}{4^2} + \frac{1}{4^2}}_{4} + \underbrace{\frac{1}{8^2} + \cdots + \frac{1}{8^2}}_{8} + \cdots \\ =&1 + \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \cdots = 2. \end{align*} Or \[ \sum_{k=1}^n \frac{1}{k^2} \leq 1 + \int_{1}^n \frac{1}{x^2} dx = 2 - \frac{1}{n} \rightarrow 2 \] as \( n \rightarrow \infty\).

  4. Consider a unit circle and a sector of angle \(\theta \in (0, \pi/2)\).

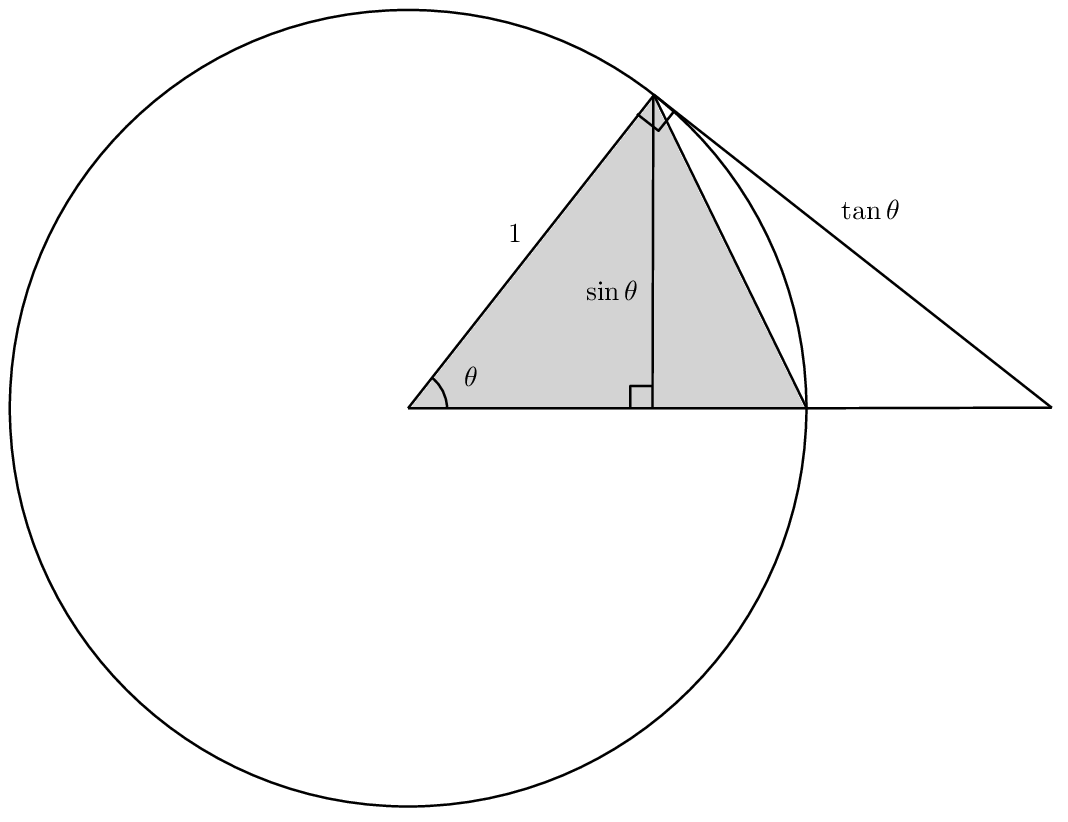
    The area of the grey inner triangle is \(\frac{1}{2} \sin \theta \). The sector of the circle of angle \(\theta\) has area \(\theta/2\). The area of the outer right-angled triangle is \(\frac{1}{2} \tan \theta\). Since each of these contain the previous one, the claimed inequalities follow.

  5. We have \[ \frac{1}{\tan^2\theta} \lt \frac{1}{\theta^2} \lt \frac{1}{\sin^2 \theta} = \frac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta} = 1 + \frac{1}{\tan^2\theta}. \]

  6. We have \[ \sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{(2n + 1)^2} \sum_{k=1}^n \frac{1}{\theta_k^2}\] and so \begin{align*} \frac{\pi^2}{(2n + 1)^2} \sum_{k=1}^n \frac{1}{\tan^2 \theta_k} \lt \sum_{k=1}^n \frac{1}{k^2} &\lt \frac{\pi^2}{(2n + 1)^2}\sum_{k=1}^n \left(\frac{1}{\tan^2\theta_k} + 1 \right) \\ &= \frac{\pi^2}{(2n + 1)^2} \sum_{k=1}^n \frac{1}{\tan^2\theta_k} + \frac{n \pi^2}{(2n + 1)^2}. \end{align*}
  7. Since \( (r_k)_{1 \leq k \leq n} \) are the roots of the polynomial, we have \[ \sum_{k=1}^n r_k = \frac{2n+1 \choose 3}{2n+1 \choose 1} = \frac{(2n+1)(2n)(2n-1)}{6(2n+1)} = \frac{2n(2n-1)}{6}.\] So \[ \frac{\pi^2}{(2n+1)^2} \sum_{k=1}^n r_k = \frac{2n(2n-1)\pi^2}{6 (2n + 1)^2} \rightarrow \frac{\pi^2}{6} \] as \( n \rightarrow \infty\). Since \[ \frac{n \pi^2}{(2n + 1)^2} \rightarrow 0, \] it follows that \(\sum_{k=1}^n \frac{1}{k^2} \) is boudned above and below by quantities which tend to \(\pi^2/6\) and the result follows.

Comments

What we have called \(Z(s) \) in this problem is of course the famous Riemann zeta function, \( \zeta(s) \). The calculation of \( Z(2) \) is known as the Basel problem. Euler first gave a non-rigorous argument in 1735. This question is based on Cauchy's (rigorous!) proof from 1821.

  1. We were expecting \(Z(s) \gt 1\) to be straightforward; it usually wasn't, and often required quite a lot of discussion.
  2. Quite often people recognised the harmonic series. Some knew that \( H_n \sim \log n\); others didn't. We often spent the bulk of time deriving a proof of this.
  3. We skipped Part 3 if the previous part had taken too long in order to give candidates a chance at something else.
  4. We rarely got beyond the fourth part on this question.