5.3 Technical Details
This section gives some of the theory behind the compression techniques
and, in general, the way FDR works.
5.3.1 Generalised Transition Systems
The operational behaviour of a CSP process can be presented as a
transition system [Scat98].
A transition system is usually deemed to be a set of (effectively)
structureless nodes which have visible or
 transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism —
which is what the refusals information conveys — by annotations on the
node.
This is a labelled transition system.
transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism —
which is what the refusals information conveys — by annotations on the
node.
This is a labelled transition system.
There is a duality between refusals (what events a state may not
engage in) and acceptances (what events a state must engage in,
if its environment desires): the one is the complement of the other in
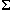 ,the universe of discourse.
As components may operate only in a small subset of
,the universe of discourse.
As components may operate only in a small subset of
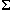 ,and as it is inclusion between maximal refusals — which corresponds to
reverse inclusion between minimal acceptances — which must be checked,
it appears to be more efficient to retain minimal acceptance
information.
,and as it is inclusion between maximal refusals — which corresponds to
reverse inclusion between minimal acceptances — which must be checked,
it appears to be more efficient to retain minimal acceptance
information.
We therefore allow nodes to be enriched by a set of minimal acceptance
sets and a divergence labelling.
We require that there be functions that map the nodes of a
generalised transition system as follows:
A node P in a generalised transition system can have multiple
actions with the same label, just as in a standard transition system.
These two properties, together with the initials (possible
visible transitions) and afters (set of states reachable after a
given event) are the fundamental properties of a node in the FDR
representation of a state-machine.
5.3.2 State-space Reduction
We mentioned earlier that one of the advances this second-generation
version of FDR offers is the ability to build up a system gradually,
at each stage compressing the subsystems to find an equivalent process
with (hopefully) many fewer states. This is one of the ways (and the
only one which is expected to be released in the immediate future) in
which implicit model-checking capabilities have been added to
FDR.
By these means we can certainly rival the sizes of systems analysed by
BDD’s (see [Clarke90], for example), though like the latter, our
implicit methods will certainly be sensitive to what example they are
applied to and how skillfully they are used.
Hopefully the examples later in these sections will illustrate this.
The idea of compressing systems as they are constructed is not new, and
indeed it has been used to a very limited extent in FDR for several
years (bisimulation is used to compact the leaf processes).
What is new is that the nature of CSP equivalences is exploited to
achieve far better compressions in some cases than can be achieved using
other, stronger equivalences.
These sections summarise the main compression techniques implemented so
far in the FDR refinement engine and give some indications of their
efficiency and applicability.
Further details can be found in [RosEtAl95].
The concept of a Generalised Labelled Transition System (GLTS) combines
the features of a standard labelled transition system and those of the
normal-form transition systems used in FDR1 to represent
specification processes [Roscoe94].
Those normalised machines are (apart from the nondeterminism coded in
the labellings) deterministic in that there are no
 actions and each node has at most one successor under each
a
actions and each node has at most one successor under each
a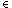
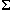
The structures of a GLTS allow us to combine the behaviour of all the
nodes reachable from a single P under
 actions into one node:
actions into one node:
-
The new node’s visible actions are just the visible transitions (with
the same result state) possible for any Q such that
P
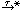 Q.
Q.
-
Its minimal acceptances are the smallest sets of visible actions
accepted by any stable Q such that
P
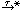 Q.
Q.
-
It is labelled divergent if, and only if, there is an infinite
 -path(invariably containing a loop, in a finite graph) from P.
-path(invariably containing a loop, in a finite graph) from P.
-
The new node has no
 actions.
actions.
Two things should be pointed out immediately:
-
While the above transformation is valid for all the standard CSP
equivalences, it is not for most stronger equivalences such as refusal
testing and observational/bisimulation equivalence.
To deal with one of these either a richer structure of node, or less
compression, would be needed.
-
It is no good simply carrying out the above transformation on each node
in a transition system.
It will result in a
 -freeGLTS, but one which probably has as many (and more complex) nodes than
the old one.
Just because
P
-freeGLTS, but one which probably has as many (and more complex) nodes than
the old one.
Just because
P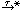 Q.and Q’s behaviour has been included in the compressed version of
P, this does not mean we can avoid including a compressed version
of Q as well: there may well be a visible transition that leads
directly to Q.
One of the main strategies discussed below — diamond elimination —
is designed to analyse which of these Q’s can, in fact, be
avoided.
Q.and Q’s behaviour has been included in the compressed version of
P, this does not mean we can avoid including a compressed version
of Q as well: there may well be a visible transition that leads
directly to Q.
One of the main strategies discussed below — diamond elimination —
is designed to analyse which of these Q’s can, in fact, be
avoided.
FDR is designed to be highly flexible about what sort of transition
systems it can work on.
We will assume, however, that it is always working with GLTS ones which
essentially generalise them all.
The operational semantics of CSP have to be extended to deal with the
labellings on nodes: it is straightforward to construct the rules that
allow us to infer the labelling on a combination of nodes (under some
CSP construct) from the labellings on the individual ones.
5.3.2.1 Computing semantic equivalence
Two nodes that are identified by strong node-labelled bisimulation are
always semantically equivalent in each of our models.
The models do, however, represent much weaker equivalences and there may
well be advantages in factoring the transition system by the appropriate
one.
The only disadvantage is that the computation of these weaker
equivalences is more expensive: it requires an expensive form of
normalisation, so
-
there may be systems where it is impractical, or too expensive, to
compute semantic equivalence, and
-
when computing semantic equivalence, it will probably be to our
advantage to reduce the number of states using other techniques first
(see section Combining techniques).
To compute the semantic equivalence relation we require the entire
normal form of the input GLTS T.
This is the normal form that includes a node equivalent to each node of
the original system, with a function from the original system which
exhibits this equivalence (the map need neither be injective [because
it will identify nodes with the same semantic value] nor surjective
[because the normal form sometimes contains nodes that are not
equivalent to any single node of the original transition system]).
Calculating the entire normal form is more time-consuming that ordinary
normalisation.
The latter begins its normalisation search with a single set (the
 -closureof T’s root,
-closureof T’s root,
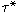 (R)),but for the entire normal form it has to be seeded with
{
(R)),but for the entire normal form it has to be seeded with
{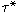 (N) |
N
(N) |
N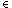 T}— usually as many sets as there are nodes in T(14).
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows:
T}— usually as many sets as there are nodes in T(14).
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows:
-
For the traces model, neither minimal acceptance nor divergence
labelling is used for the bisimulation.
-
For the stable failures model, only minimal acceptance labelling is
used.
-
For the failures-divergences model, both sorts of labelling are used and
in the pre-normalisation phase there is no need to search beyond a
divergent node.
The map from T to the normal form is then just the composition of
that which takes N to the pre-normal form node
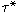 (N),and the final bisimulation.
(N),and the final bisimulation.
The equivalence relation is then simply that induced by the map: two
nodes are equivalent if and only if they are mapped to the same node in
the normal form.
5.3.2.2 Diamond elimination
This procedure assumes that the relation of
 -reachibilityis a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
-reachibilityis a partial order on nodes.
If the input transition system is known to be divergence free then this
is true, otherwise
 -loopelimination is required first (since this procedure guarantees to
achieve the desired state).
-loopelimination is required first (since this procedure guarantees to
achieve the desired state).
Under this assumption, diamond reduction can be described as follows,
where the input state-machine is S (in which nodes can be marked
with information such as minimal acceptances), and we are creating a new
state-machine T from all nodes explored in the search:
-
Begin a search through the nodes of S starting from its root
N0.At any time there will be a set of unexplored nodes of S; the search
is complete when this is empty.
-
To explore node N, collect the following information:
- -
The set
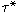 (N)of all nodes reachable from N under a (possibly empty) sequence
of
(N)of all nodes reachable from N under a (possibly empty) sequence
of
 actions.
actions.
- -
Where relevant (based on the equivalence being used), divergence and
minimal acceptance information for N: it is divergent if any
member of
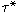 (N)is either marked as divergent or has a
(N)is either marked as divergent or has a
 to itself.
The minimal acceptances are the union of those of the members of
to itself.
The minimal acceptances are the union of those of the members of
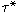 (N)with non-minimal sets removed.
This information is used to mark N in T.
(N)with non-minimal sets removed.
This information is used to mark N in T.
- -
The set V(N) of initial visible actions: the union of the set of
all
non-
 actions possible for any member of
actions possible for any member of
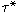 (N).
(N).
- -
For each
a
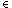 V(N),the set
Na = N after aof all nodes reachable under a from any member of
V(N),the set
Na = N after aof all nodes reachable under a from any member of
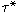 (N).
(N).
- -
For each a
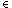 V(N), the set
min(Na) which is the set of all
V(N), the set
min(Na) which is the set of all
 -minimal elements of
Na (i.e., those nodes not reachable under
-minimal elements of
Na (i.e., those nodes not reachable under
 from any other in
Na).
from any other in
Na).
-
A transition (labelled a) is added to T from N to each
N’ in
min(Na), for all
a
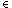 V(N).Any nodes not already explored are added to the search.
V(N).Any nodes not already explored are added to the search.
This creates a transition system where there are no
 -actionsbut where there can be ambiguous branching under visible actions, and
where nodes might be labelled as divergent.
The reason why this compresses is that we do not include in the search
nodes where there is another node similarly reachable but demonstrably
at least as nondeterministic: for if
M
-actionsbut where there can be ambiguous branching under visible actions, and
where nodes might be labelled as divergent.
The reason why this compresses is that we do not include in the search
nodes where there is another node similarly reachable but demonstrably
at least as nondeterministic: for if
M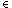
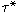 (N)then N is always at least as nondeterministic as M.
The hope is that the completed search will tend to include only those
nodes that are
(N)then N is always at least as nondeterministic as M.
The hope is that the completed search will tend to include only those
nodes that are
 -minimal in
T.Notice that the behaviours of the nodes not included from
Naare nevertheless taken account of, since their divergences and minimal
acceptances are included when some node of
min(Na)is explored.
-minimal in
T.Notice that the behaviours of the nodes not included from
Naare nevertheless taken account of, since their divergences and minimal
acceptances are included when some node of
min(Na)is explored.
It seems counter-intuitive that we should work hard not to unwind
 'srather than doing so eagerly.
The reason why we cannot simply unwind
'srather than doing so eagerly.
The reason why we cannot simply unwind
 'sas far as possible (i.e., collecting the
'sas far as possible (i.e., collecting the
 -maximalpoints reachable under a given action) is that there will probably be
visible actions possible from the unstable nodes we are trying to
bypass.
It is impossible to guarantee that these actions can be ignored.
-maximalpoints reachable under a given action) is that there will probably be
visible actions possible from the unstable nodes we are trying to
bypass.
It is impossible to guarantee that these actions can be ignored.
The reason we have called this compression diamond elimination is
because what it does is to (attempt to) remove nodes based on the
diamond-shaped transition arrangement where we have four nodes
P, P’, Q, Q’ and
P 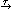 P',
Q
P',
Q 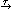 Q',
P
Q',
P 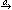 Q and
P'
Q and
P' 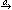 Q'.Starting from P, diamond elimination will seek to remove the
nodes P’ and Q’.
The only way in which this might fail is if some further node in the
search forces one or both to be considered.
Q'.Starting from P, diamond elimination will seek to remove the
nodes P’ and Q’.
The only way in which this might fail is if some further node in the
search forces one or both to be considered.
A Lemma in [RosEtAl95] shows that the following two types of node are
certain to be included in T:
-
The initial node
N0.
-
S0,the set of all
 -minimalnodes (ones not reachable under
-minimalnodes (ones not reachable under
 from any other).
from any other).
Let us call
S0
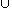 {N0}the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
{N0}the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
Experimentation over a wide range of example CSP processes has
demonstrated that diamond elimination is a highly effective compression
technique, with success ratings usually at or close to 100% on most
natural systems.
To illustrate how diamond elimination works, consider one of the most
hackneyed CSP networks: N one-place buffer processes chained
together.
COPY 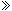 COPY
COPY 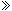 ...
COPY
...
COPY 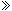 COPY
COPY
Here,
COPY=left?x 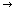 right!x
right!x 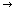 COPY.If the underlying type of (the communications on) channel left
(and right) has k members then COPY has k+1
states and the network has
(k+1) N [k+1 to the power N].Since all of the internal communications (the movement of data from one
COPY to the next) become
COPY.If the underlying type of (the communications on) channel left
(and right) has k members then COPY has k+1
states and the network has
(k+1) N [k+1 to the power N].Since all of the internal communications (the movement of data from one
COPY to the next) become
 actions, this is an excellent target for diamond elimination.
And in fact we get 100% success: the only nodes retained are those that
are not
actions, this is an excellent target for diamond elimination.
And in fact we get 100% success: the only nodes retained are those that
are not
 -reachablefrom any other.
These are the ones in which all of the data is as far to the left as it
can be: there are no empty COPY’s to the left of a full one.
If k=1 this means there are now N+1 nodes rather than
2 N [2 to the power N],and if k=2 it gives
2 N+1 -1 [one less than 2 to the power N+1]
rather than 3 N [3 to the power N].
-reachablefrom any other.
These are the ones in which all of the data is as far to the left as it
can be: there are no empty COPY’s to the left of a full one.
If k=1 this means there are now N+1 nodes rather than
2 N [2 to the power N],and if k=2 it gives
2 N+1 -1 [one less than 2 to the power N+1]
rather than 3 N [3 to the power N].
5.3.2.3 Combining techniques
The objective of compression is to reduce the number of states in the
target system as much as possible, with the secondary objectives of
keeping the number of transitions and the complexity of any minimal
acceptance marking as low as possible.
There are essentially two possibilities for the best compression of a
given system: either its normal form or the result of applying some
combination of the other techniques.
For whatever equivalence-preserving transformation is performed on a
transition system, the normal form (from its root node) must be
invariant; and all of the other techniques leave any normal form system
unchanged.
In many cases (such as the chain of COPYs above) the two will be
the same size (for the diamond elimination immediately finds a system
equivalent to the normal form, as does equivalence factoring), but there
are certainly cases where each is better.
The relative speeds (and memory use) of the various techniques vary
substantially from example to example, but broadly speaking the relative
efficiencies are (in decreasing order)
 -loopelimination (except in rare complex cases), bisimulation, diamond
elimination, normalisation and equivalence factoring.
The last two can, of course, be done together since the entire normal
form contains the usual normal form within it.
Diamond elimination is an extremely useful strategy to carry out before
either sort of normalisation, both because it reduces the size of the
system on which the normal form is computed (and the number of seed
nodes for the entire normal form) and because it eliminates the need for
searching through chains of
-loopelimination (except in rare complex cases), bisimulation, diamond
elimination, normalisation and equivalence factoring.
The last two can, of course, be done together since the entire normal
form contains the usual normal form within it.
Diamond elimination is an extremely useful strategy to carry out before
either sort of normalisation, both because it reduces the size of the
system on which the normal form is computed (and the number of seed
nodes for the entire normal form) and because it eliminates the need for
searching through chains of
 -actionswhich forms a large part of the normalisation process.
-actionswhich forms a large part of the normalisation process.
One should note that all our compression techniques guarantee to do no
worse than leave the number of states unchanged, with the exception of
normalisation which in the worst case can expand the number of states
exponentially.
Cases of expanding normal forms are very rare in practical systems.
All of these compression techniques have been implemented and many
experiments have been performed using them.
Ultimately we expect that FDR’s compression processing will be at
least to some extent automated according to a strategy based on a
combination of these techniques, with the additional possibility of user
intervention.
This document was generated by Phil Armstrong on May 17, 2012 using texi2html 1.82.
 transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism —
which is what the refusals information conveys — by annotations on the
node.
This is a labelled transition system.
transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism —
which is what the refusals information conveys — by annotations on the
node.
This is a labelled transition system.
 ,the universe of discourse.
As components may operate only in a small subset of
,the universe of discourse.
As components may operate only in a small subset of
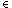 minaccs(P)if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one ‘state’ the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have
minaccs(P)if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one ‘state’ the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have
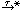 Q.
Q.
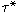 (R)),but for the entire normal form it has to be seeded with
{
(R)),but for the entire normal form it has to be seeded with
{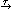 P',
Q
P',
Q 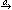 Q and
P'
Q and
P' 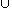 {N0}the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
{N0}the core of S.
The obvious criteria for judging whether to try diamond reduction at
all, and of how successful it has been once tried, will be based on the
core.
For since the only nodes we can hope to get rid of are the complement of
the core, we might decide not to bother if there are not enough of these
as a proportion of the whole.
And after carrying out the reduction, we can give a success rating in
terms of the percentage of non-core nodes eliminated.
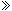 COPY
COPY 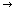 right!x
right!x