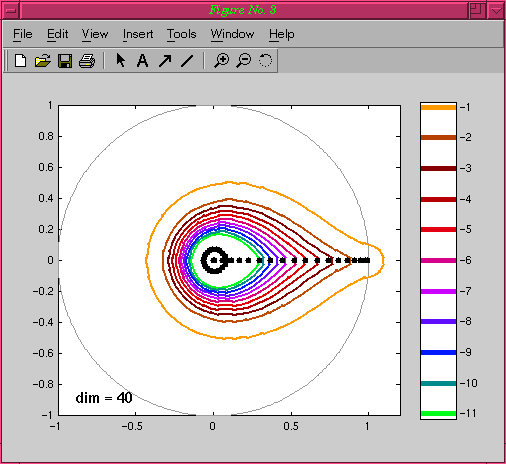
Gauss-Seidel is one of the "classic matrix iterations" analyzed first by Frankel in 1950 and incorporated into a general theory by Young in the early 1950s [1,2,3]. This demonstration applies it to three standard model problems based on discretizing a simple 1D differential equation by a tridiagonal matrix A = L+D+U. The Gauss-Seidel matrix G is obtained when the lower half of this matrix, L+D, is split from the upper half.
In the "classic" case A is the symmetric (-1,2,-1)/N^2 matrix associated with the 1D Laplace equation. The matrix G is very strongly non-normal. However, the non-normality affects the smaller eigenvalues, not the largest one, which was shown by Frankel and Young to be of order 1-N^2. This is why the Frankel-Young theory, even though it looks only at eigenvalues, matches numerical experiments.

The "downwind" and "upwind" cases come from discretizing an equation that has convection as well as diffusion. Now A is nonsymmetric and we have a choice of whether the Gauss-Seidel iteration sweeps with or against the "wind", i.e., whether the larger or the smaller half of A is split from the rest. The two choices lead to matrices G with identical eigenvalues but very different convergence behaviors as measured by norms of powers of G. For the downwind sweep, nonnormality causes little trouble and convergence matches an eigenvalue prediction from the start.
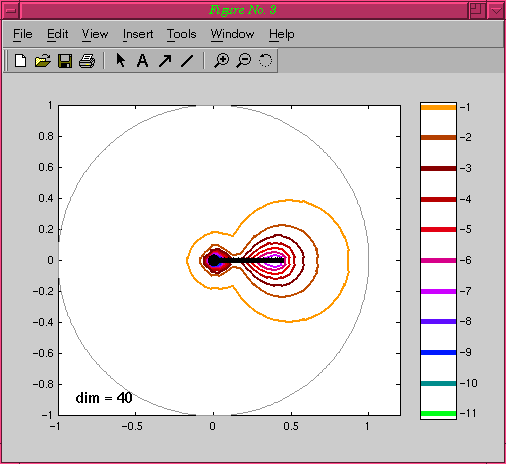
For the upwind sweep, nonnormality is dominant and there is a period of stagnation before the iteration begins to converge.
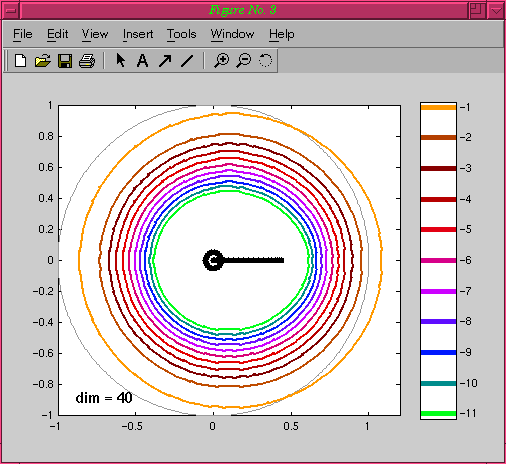
The connection of these upwind-downwind effects to pseudospectra was first pointed out in [4].
[1]: S. Frankel,"Convergence rates of iterative treatments of partial differential equations", Math. Comp. 4 (1950), 65-75.
[2]: G. H. Golub and C. F. Van Loan, "Matrix Computations", 3rd ed., Johns Hopkins U. Press, Baltimore, 1996.
[3]: R. J. LeVeque and L. N. Trefethen, "Fourier analysis of the SOR iteration," IMA J. Numer. Anal. 8 (1988), 273-279.
[4]: L. N. Trefethen, "Pseudospectra of matrices", in D. F. Griffiths and G. A. Watson, eds., Numerical Analysis 1991, Longman Scientific and Technical, Harlow, Essex, UK, 234-266, 1992.
EigTool EigTool Demos Menu.