ZX Calculus and Fault-tolerant quantum computing
Aleks Kissinger
Topos Colloquium, 2025

Quantum computing



Quantum computers encode data in quantum systems,
which enables us to do computations in totally new ways.
Quantum Software
the code that runs on a quantum computer
|
INIT 5 CNOT 1 0 H 2 Z 3 H 0 H 1 CNOT 4 2 ... |
↔ |
Quantum Software
code that makes that code (better)
 |
 |
 |
| Optimisation | Simulation & Verification | Error Correction |
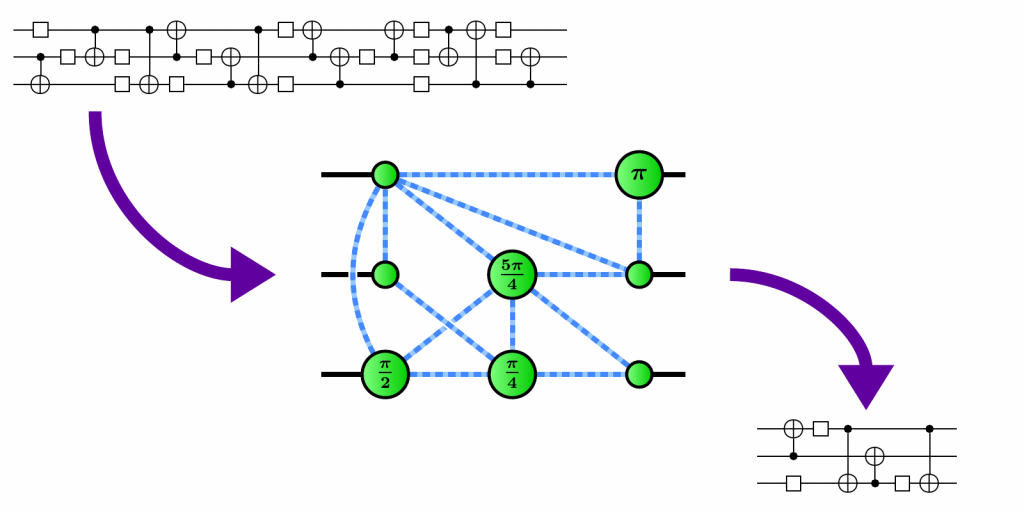
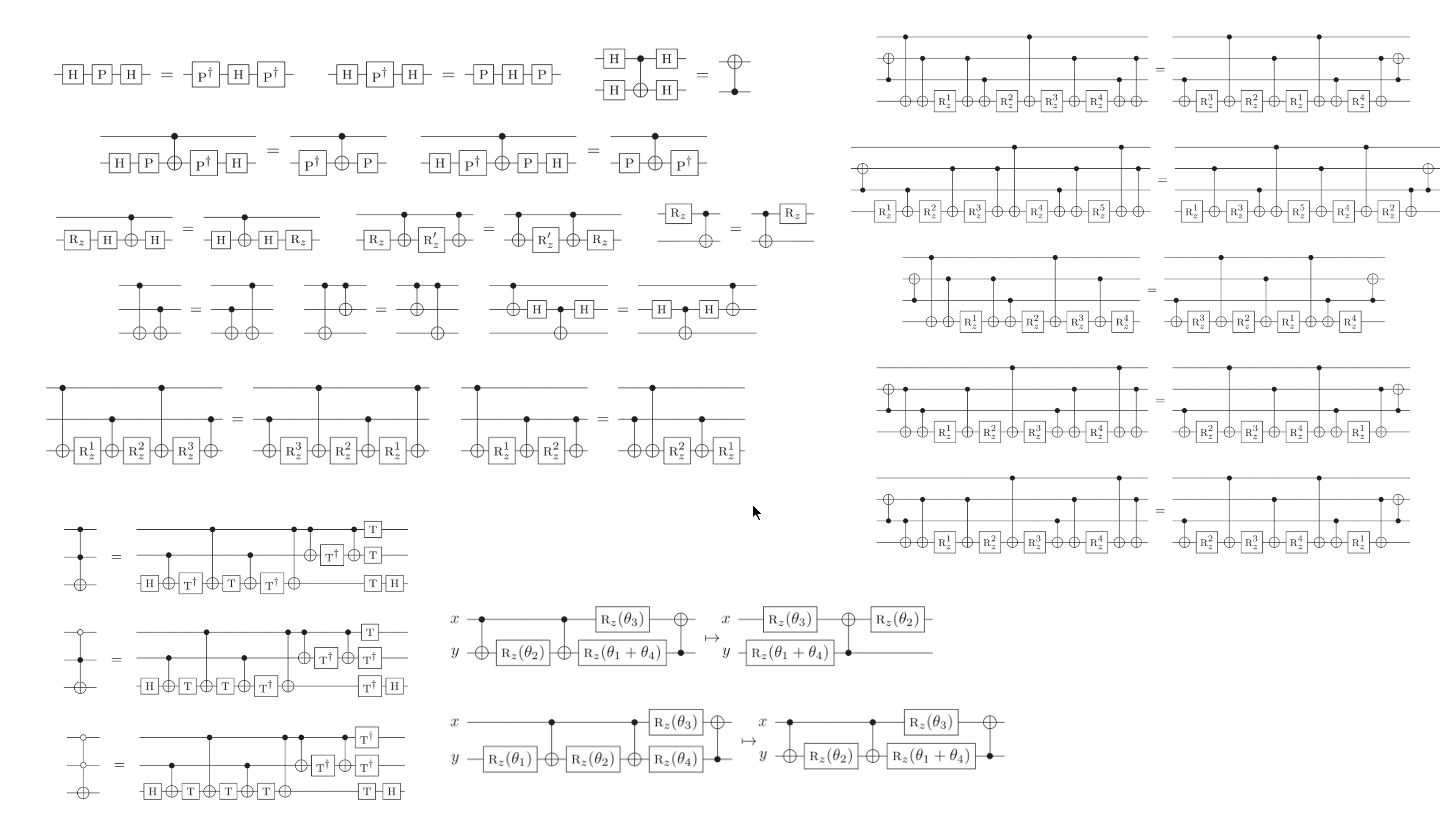
Optimising circuits the old-fashioned way
...
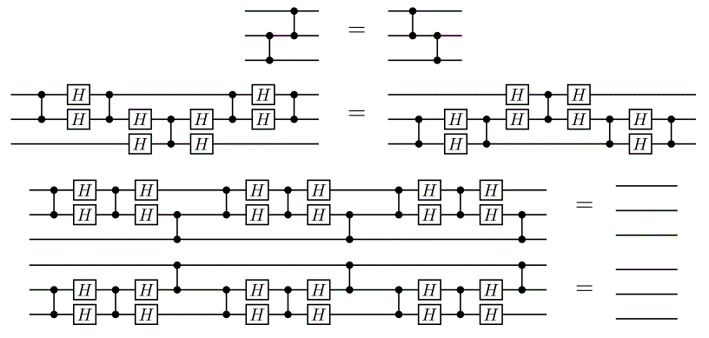
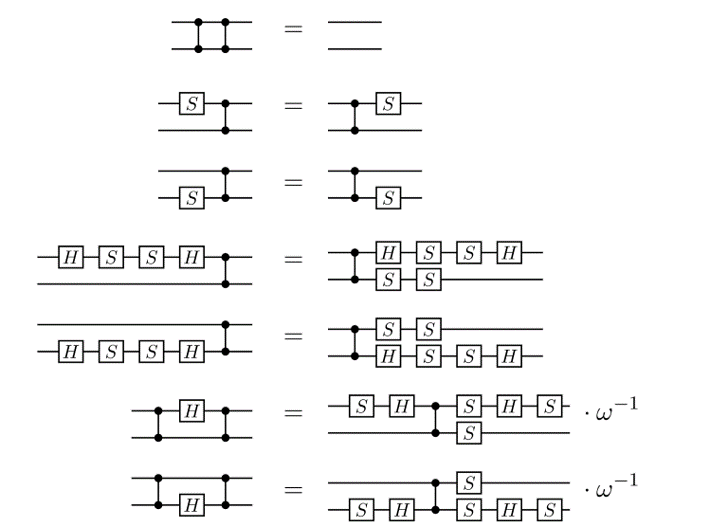
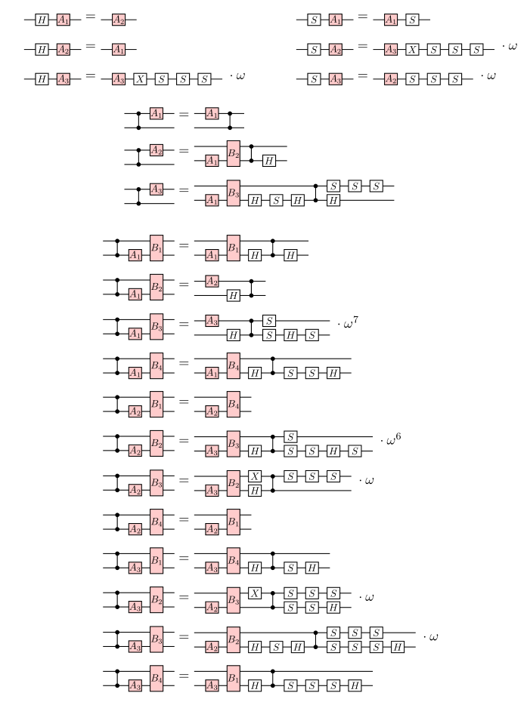
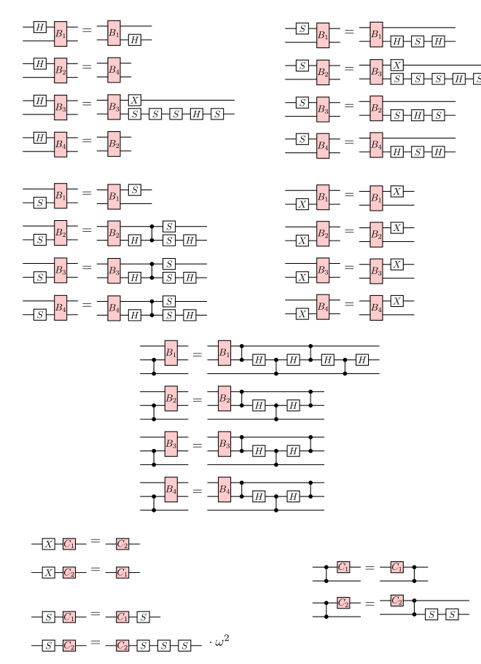
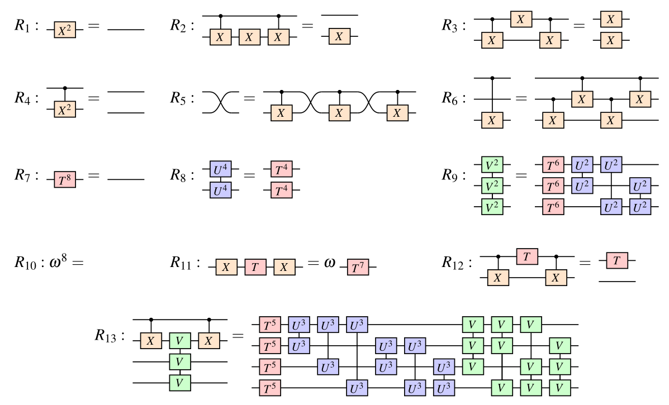
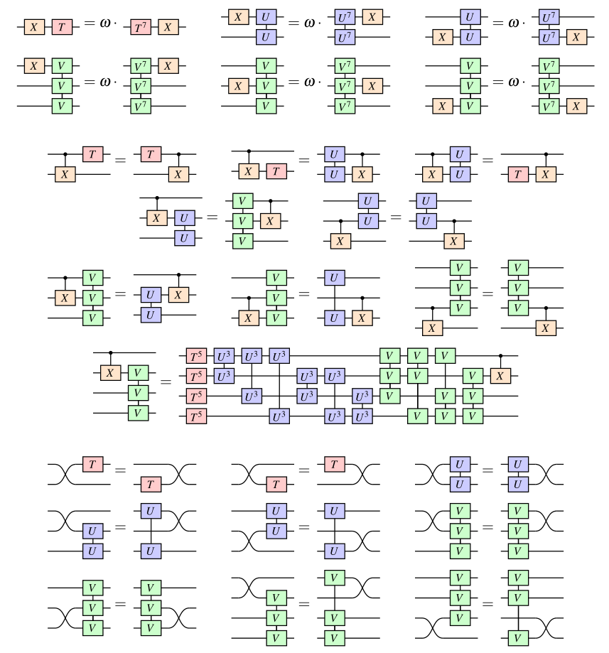
A better idea: the ZX calculus
A complete set of equations for qubit QC
PyZX
- Open source Python library for circuit optimisation, experimentation, and education using ZX-calculus
https://github.com/zxcalc/pyzx
QuiZX


- Large scale circuit optimisation and classical simulation library for ZX-calculus
https://github.com/zxcalc/quizx
ZXLive
- GUI tool based on PyZX
https://github.com/zxcalc/zxlive

https://zxcalc.github.io/book
https://zxcalculus.com
(>300 tagged ZX papers, online seminars, Discord)
Quantum errors
- Classical error rate $\approx 10^{-18}$
- Quantum error rate $10^{-2} - 10^{-5}$
- decoherence, thermal noise, crosstalk, cosmic rays, ...
- Probability of a successful (interesting) computation $\approx 0$
Quantum error correction
into a bigger space of physical qubits:
- $E$ (or just $\textrm{Im}(E)$) is a called a quantum error correcting code
- Fault-tolerant quantum computing (FTQC) requires methods for:
- encoding/decoding logical states and measurements
- measuring physical qubits to detect/correct errors
- doing fault-tolerant computations on encoded qubits
Let's see how this works...using ZX
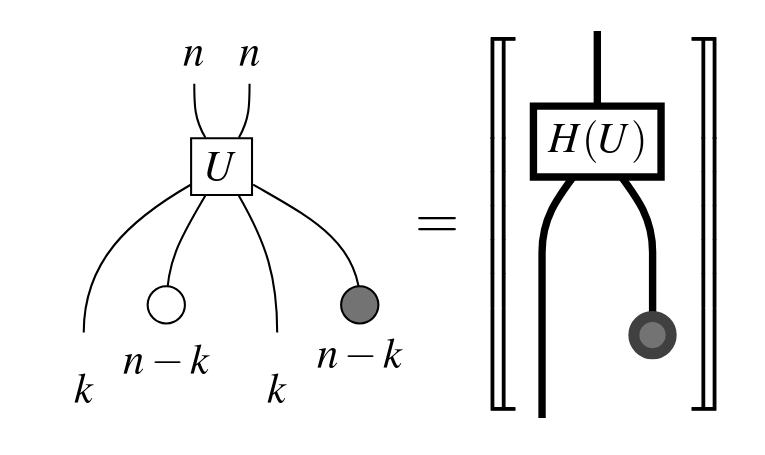
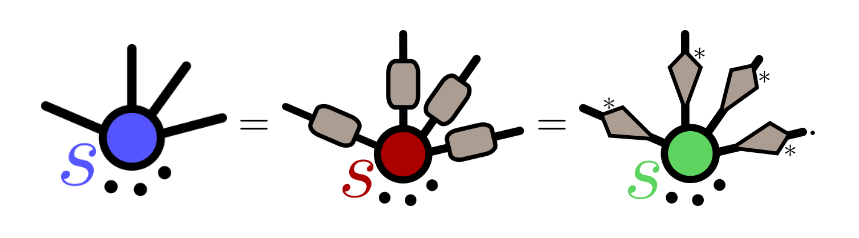
Ingredients
ZX-diagrams are made of spiders:
Spiders can be used to construct basic pieces of a computation, namely...
Quantum Gates
...which evolve a quantum state, i.e. "do" the computation:
Quantum Measurements
...which collapse the quantum state to a fixed one,
depending on the outcome $k \in \{0,1\}$:
Modelling errors
A simple classical error model assumes at each time step, a bit might get flipped with some fixed (small) probability $p$.
Generalises to qubits, accounting for the fact that
"flips" can be on different axes:
Modelling errors
Spiders of the same colour fuse together and their phases add:
$\implies$ errors will flip the outcomes of measurements of the same colour:
Detecting errors
We can try to detect errors with measurements,
but single-qubit measurements have a problem...
...they collapse the state!
Multi-qubit measurements
$n$-qubit basis vectors are labelled by bitstrings
$k=0$ projects onto "even" parity and $k=1$ onto "odd" parity
...the same, but w.r.t. a different basis
Example: GHZ code
Example: GHZ code
Example: GHZ code
giving an error syndrome.
Example: GHZ code
on a physical qubit, but it can't handle Z-flips.
Steane code
The Steane code requires 7 physical qubits, but it allows
correction of any single-qubit X, Y, or Z error
Problem:
Constructing good codes (esp. Good Codes)
- QEC codes are described by 3 parameters $[[n,k,d]]$
- $n$ - the number of physical qubits (smaller is better!)
- $k$ - the number of logical qubits (bigger is better!)
- $d$ - distance, the size of the smallest undetectable error (bigger is better!)
- e.g. the Surface Code is well understood and has many advantages, but its parameters aren't great ($k=1$, $d = \sqrt{n}$)
- OTOH Good LDPC Codes have amazing parameters ($k = \Theta(n)$, $d = \Theta(n)$), but are less well-understood
Application: canonical forms for encoders
ZX normal forms give canonical forms for encoders, enable convenient expressions of equiv. classes of codes and machine search.
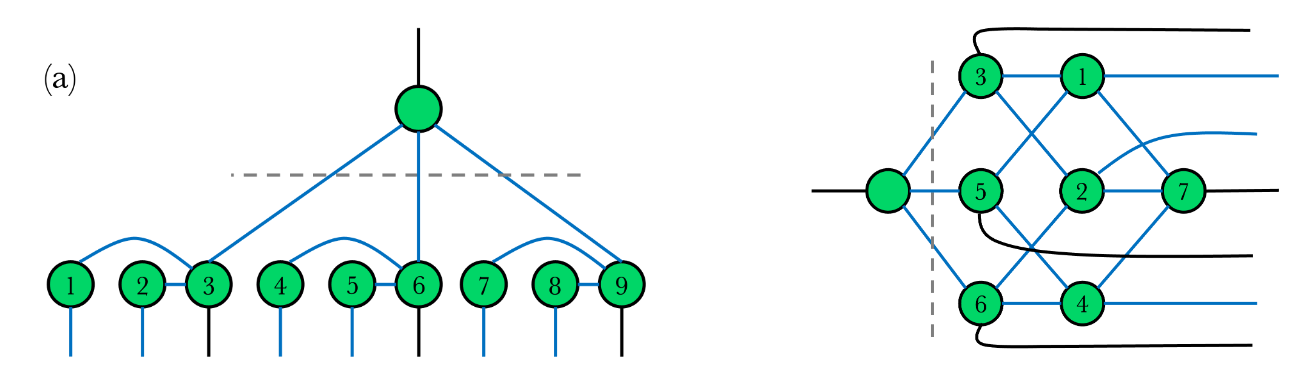

arXiv:2301.02356 | arXiv:2406.12083
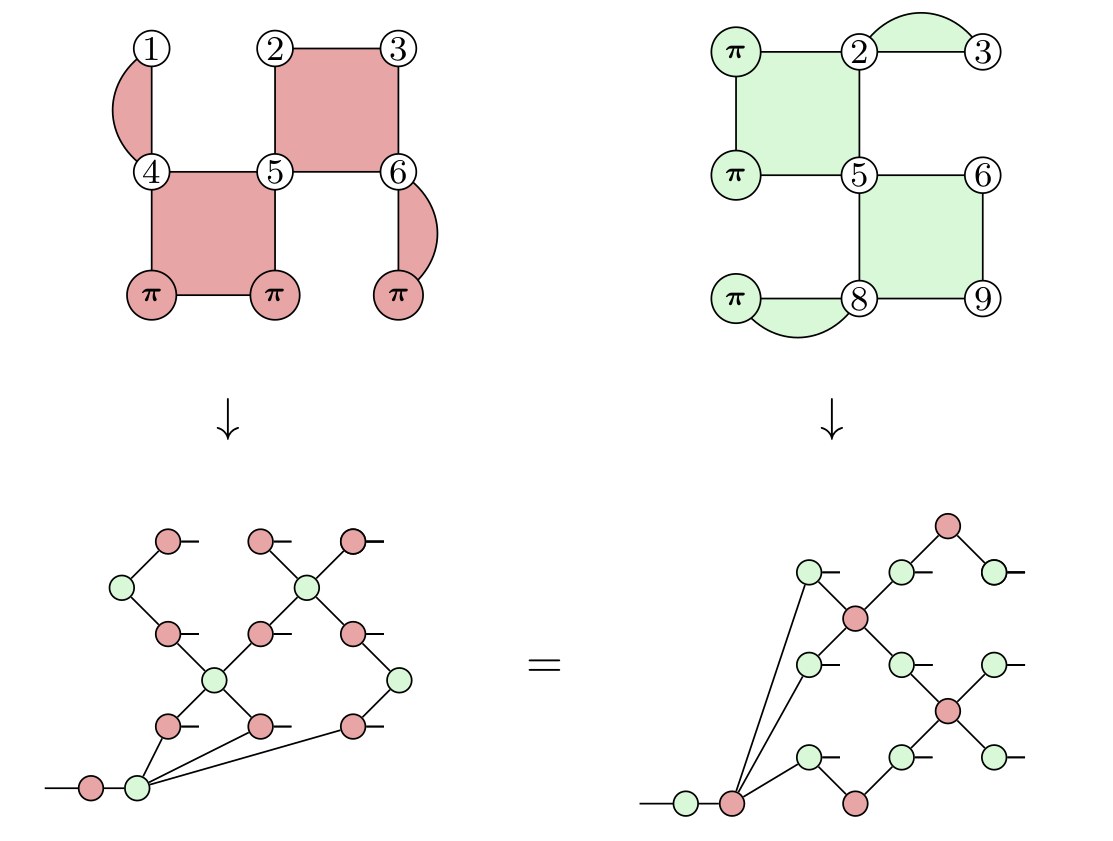
Application: concatenated graph codes
Clifford ZX-calculus enables computing the
graph code of a concatenated graph code:
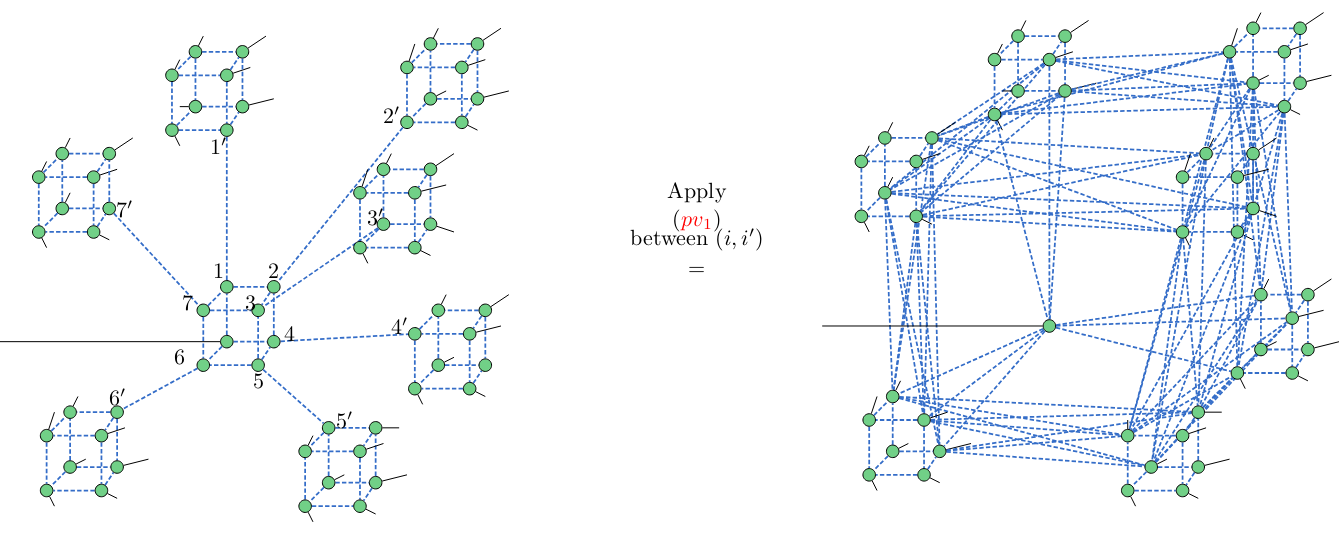
arXiv:2304.08363
Application: QEC code transformations
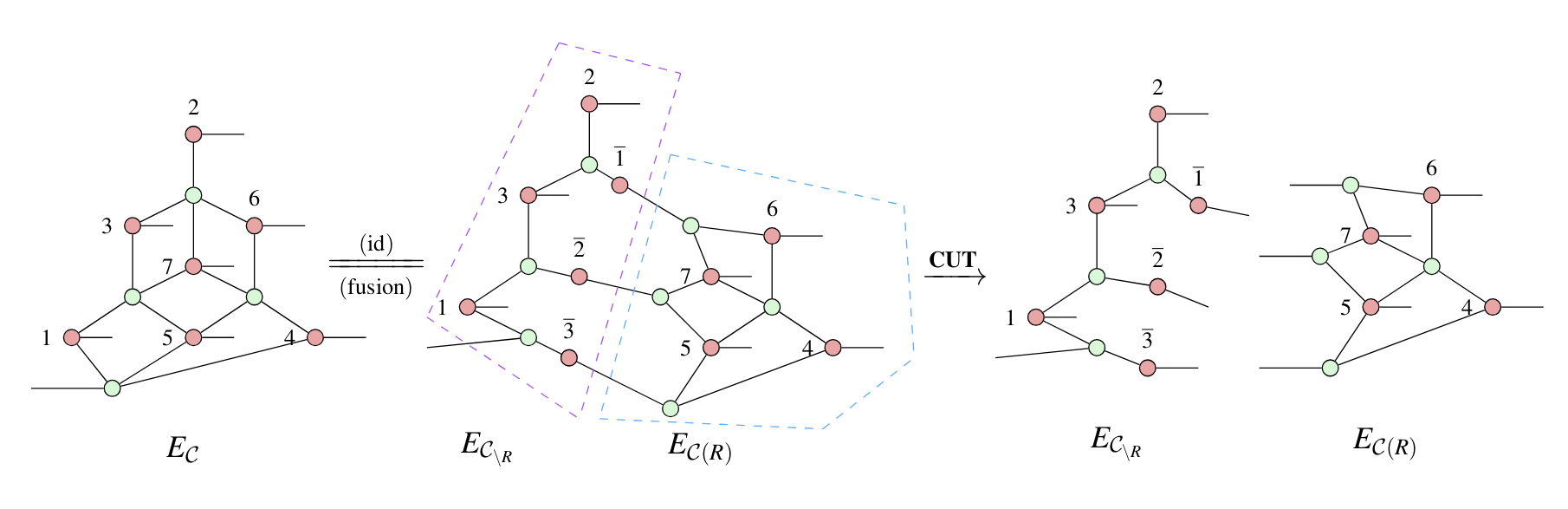
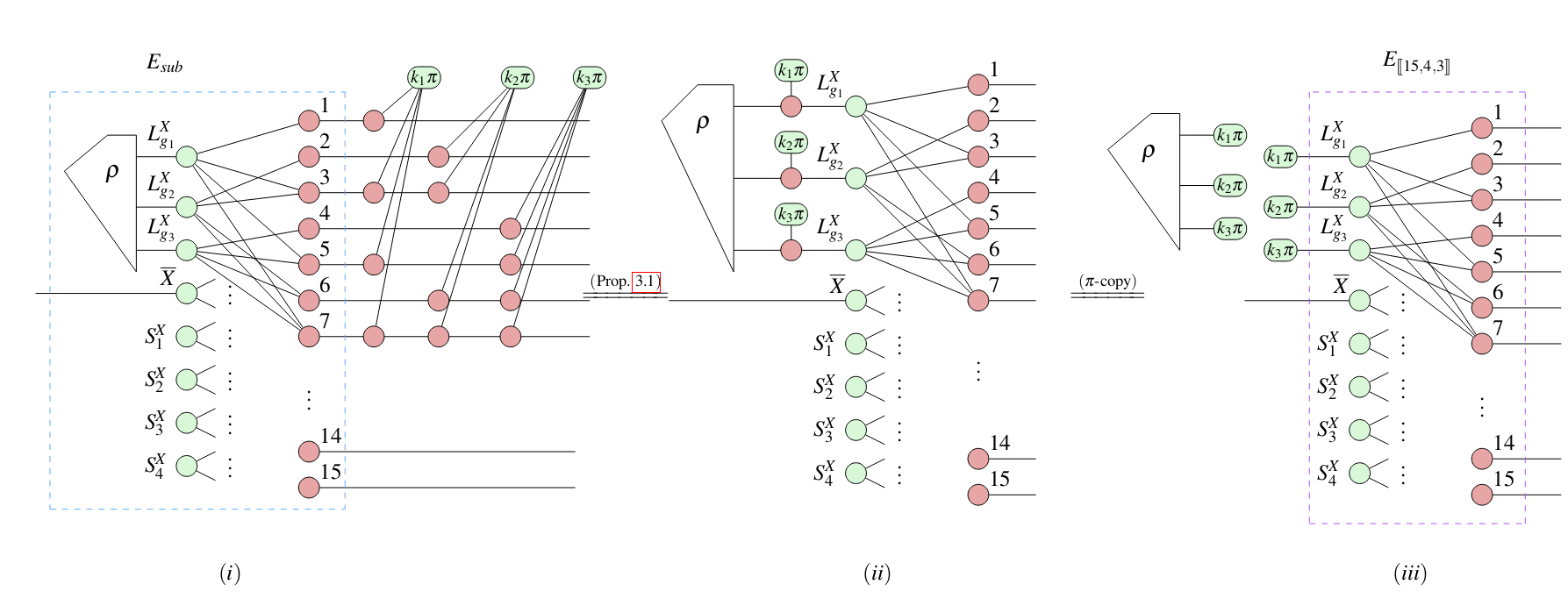
arXiv:2307.02437
Problem:
Fault-tolerant quantum computing
Q: How do we perform computations and measurements on encoded quantum data without ruining the QEC properties?When things go wrong
Consider a 4-qubit parity measurement:
How can we implement this?
When things go wrong
ZX can give us an answer:
Q: Is the LHS really equivalent to the RHS?
A: It depends on what "equivalent" means.
When things go wrong
They both give the same linear map, i.e. the behave the same in the absence of errors.
But they behave differently in the presence of errors, e.g.
Solution: Finer-grained equivalence
Definition:
Two circuits (or ZX-diagrams) $C, D$ are called fault-equivalent, written:
$C \hat{=} D$
if for any undetectable fault $f$ of weight $w$ on $C$, there exists an undetectable fault $f'$ of weight $\leq w$ on $D$ such that $C[f] = D[f']$ (and vice-versa).Fault-equivalence
- While all the ZX rules preserve map-equivalence, only some rules preserve fault-equivalence.
- It turns out the ones that do, e.g.
...are very useful for compiling fault-tolerant circuits!
Paradigm: Fault-tolerance by construction
Idea: start with an idealised computation (i.e. specification) and refine it with fault-equivalent rewrites until it is implementable on hardware.
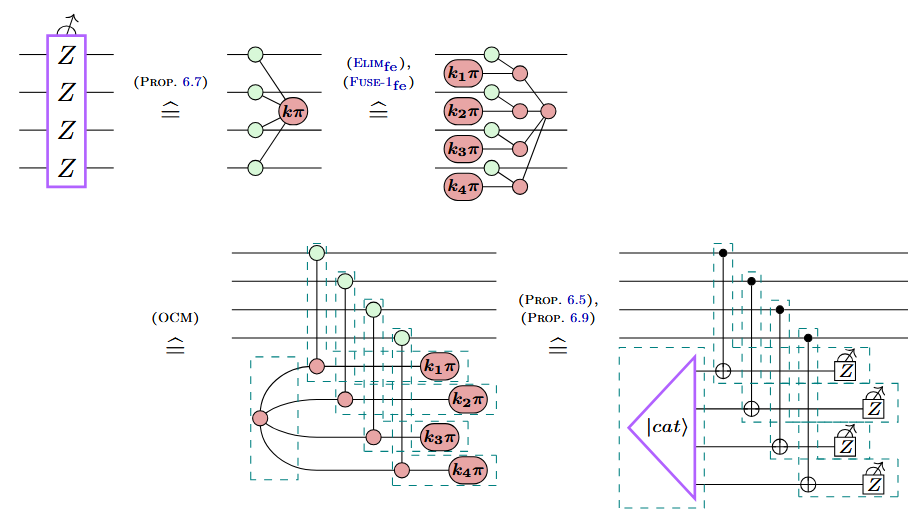
Shor-style syndrome extraction
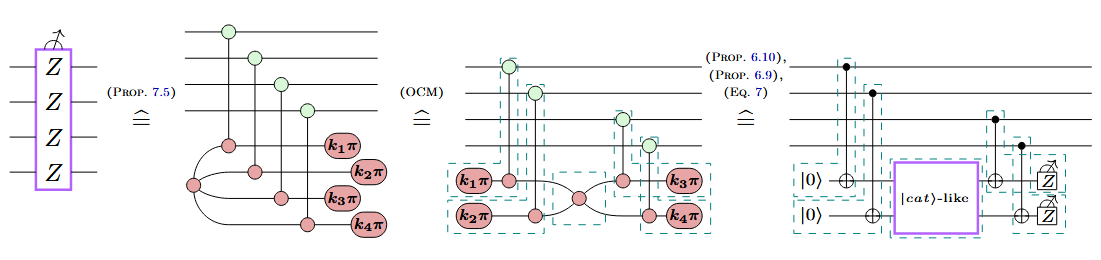
a new variation on Shor
Where to?
- Constructing efficient/useful FT circuits.
- Automated compiling with fault-equivalent rewriting (e.g. using heuristic search/ML).
- Automated checking of fault-equivalence for ZX diagrams (exponential in general, but there seem to be some shortcuts...).
- Rewrites that preserve efficient decodability of errors from syndromes (NP/#P-hard in general, but efficient algorithms exist for many codes).
- A complete set of fault-equivalent rewrites?
More ZX+QEC
A lot has happened in the past few years, see:
zxcalculus.com/publications.html?q=error%20correcting%20codesSome highlights...
Application: lattice surgery
arXiv:2204.14038
 » PQS, Chapter 11
» PQS, Chapter 11
Application: unifying FTQC
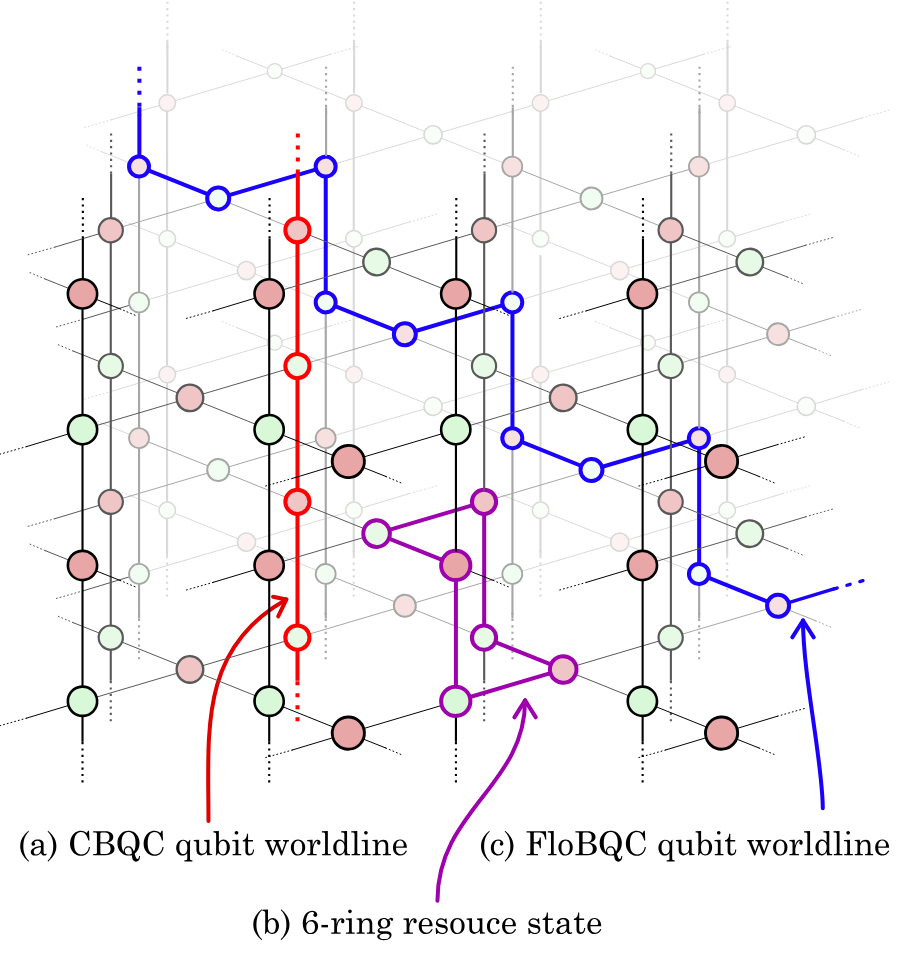
arXiv:2303.08829 (PsiQuantum)
Application: active volume
a ZX-based paradigm for fault-tolerance well-suited to photonic qubits
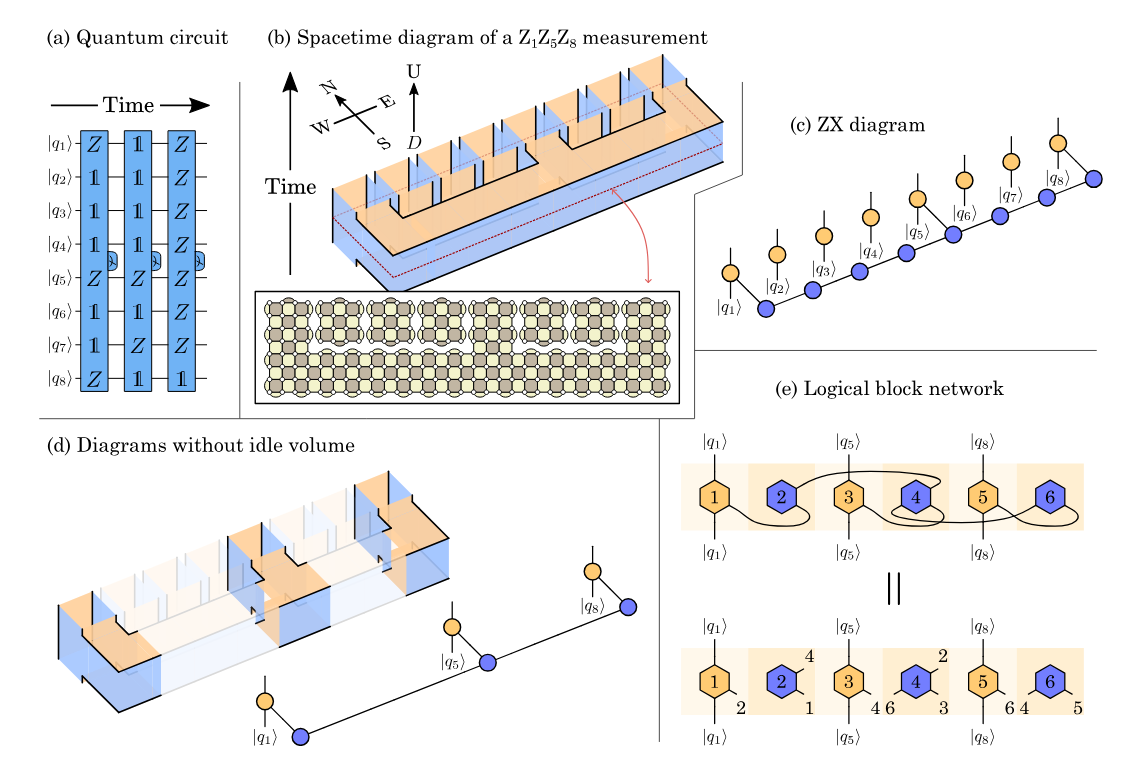
arXiv:2211.15465 (PsiQuantum)
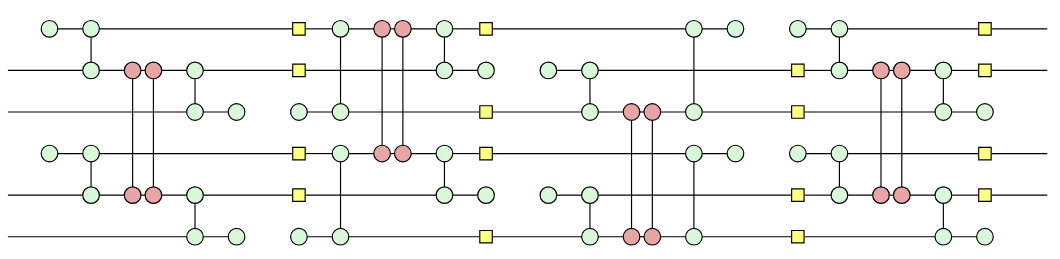
Application: Floquetification
Fault-equivalent rewrites from stabiliser codes to Floquet codes
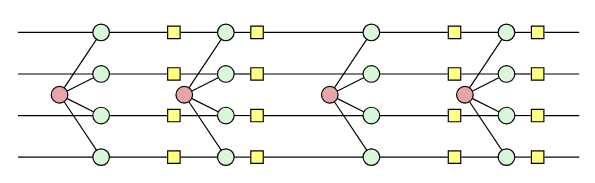 $\leadsto$
$\leadsto$
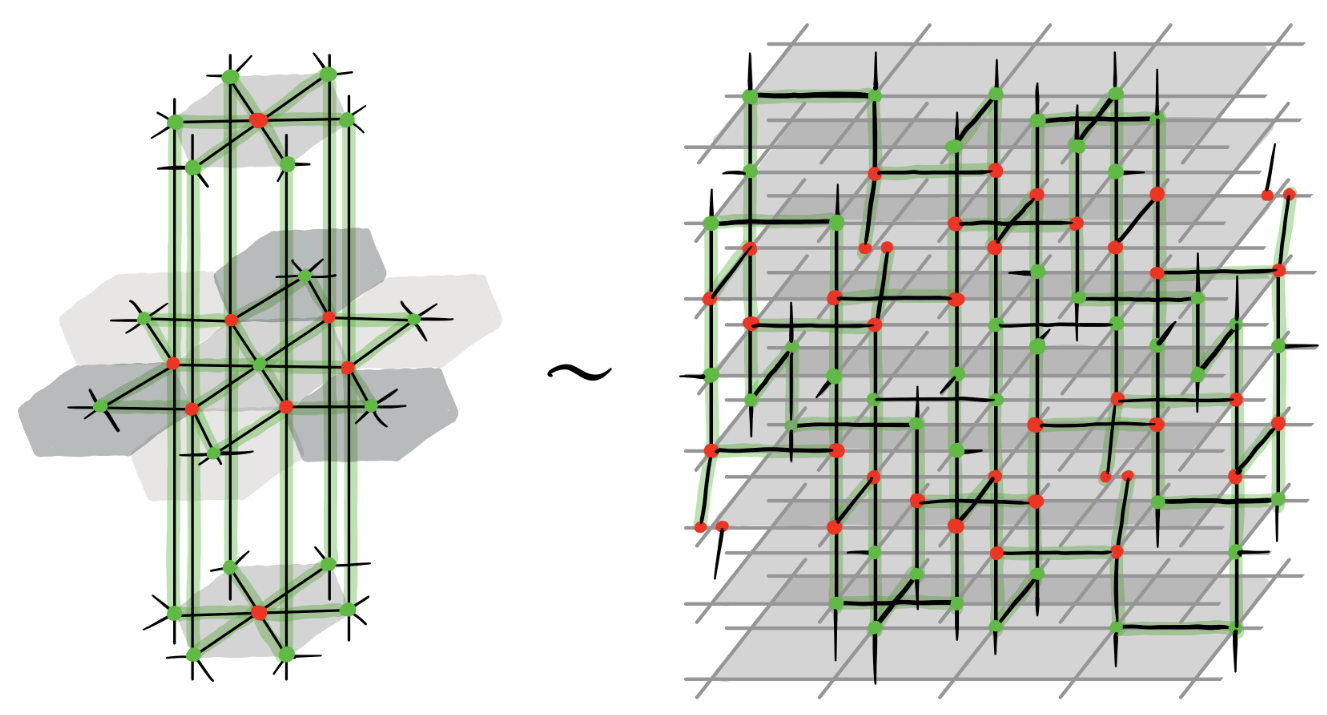
...and more
 |
 |
 |
| Quopit stabiliser codes with graphical symplectic algebra | XYZ ruby codes with 3-color ZX variation |
Genon codes |
| arXiv:2304.10584 | arXiv:2407.08566 | arXiv:2406.09951 |