Quantum Error Correction and Fault Tolerance...
Aleks Kissinger
Topics in Quantum Informatics, 2025

...with Pictures!
ZX-calculus := a handy tool for working with quantum
computations using graph rewriting
 |
 |
 |
| Optimisation | Simulation & Verification | Error Correction |
Optimising circuits the old-fashioned way
A better idea: decompose a circuit into a ZX diagram
ZX diagrams
- Gates are represented using more basic building blocks, called spiders:
$:=$ $\ \ |0...0\rangle\langle 0...0| + e^{i \alpha} |1...1\rangle\langle 1...1|$ $:=$ $\ \ |{+}...{+}\rangle\langle {+}...{+}| + e^{i \alpha} |{-}...{-}\rangle\langle {-}...{-}|$ - E.g.
$\textit{CNOT} :=$
$\sqrt{X} :=$
$Z_\alpha :=$
- Wire order doesn't matter $\Rightarrow$ treat ZX-diagrams as undirected graphs
...then use the ZX calculus
A complete set of equations for qubit QC
 PyZX
PyZX
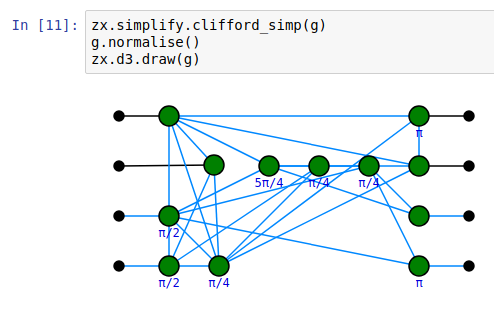
- Open source Python library for circuit optimisation, experimentation, and education using ZX-calculus
https://github.com/zxcalc/pyzx
 QuiZX
QuiZX

- Large scale circuit optimisation and classical simulation library for ZX-calculus
https://github.com/zxcalc/quizx
 ZXLive
ZXLive
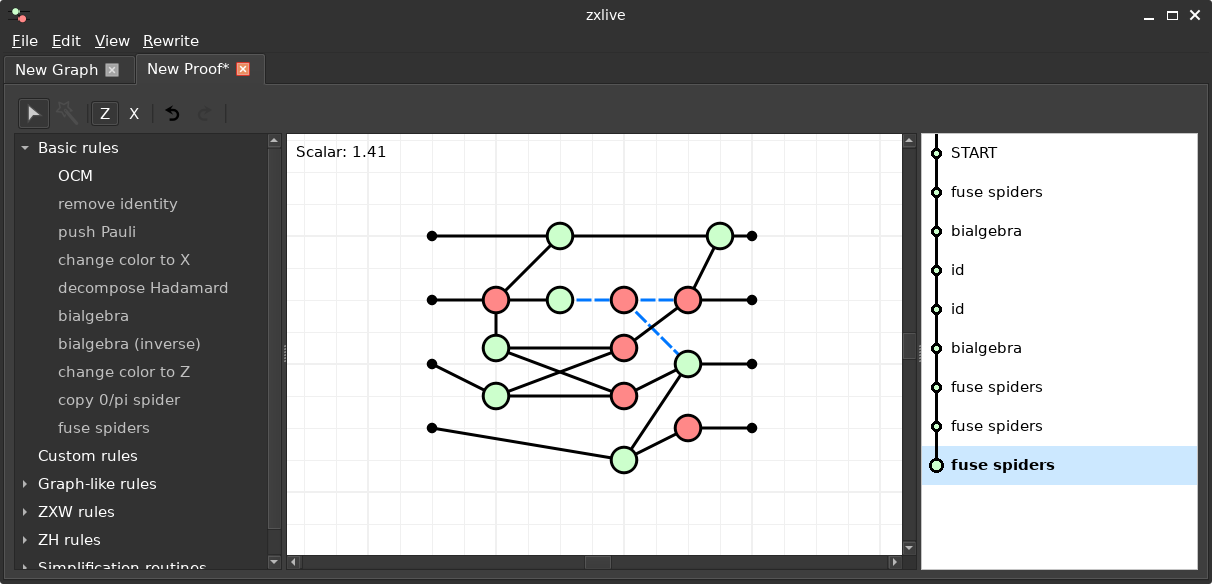
- GUI tool based on PyZX
https://github.com/zxcalc/zxlive
Quantum errors
- Classical error rate $\approx 10^{-18}$
- Quantum error rate $10^{-2} - 10^{-5}$
- decoherence, thermal noise, crosstalk, cosmic rays, ...
- Probability of a successful (interesting) computation $\approx 0$
Quantum error correction
Currently there are no persuasive theoretical arguments indicating that commercially viable applications will be found that do not use quantum error-correcting codes and fault-tolerant quantum computing.
- John Preskill, Q2B Keynote 2023
Quantum error correction
...is done by encoding some space of logical qubitsinto a bigger space of physical qubits:
- $E$ defines a quantum error correcting code
- Fault-tolerant quantum computing (FTQC) consists of:
- encoding/decoding logical states and measurements
- measuring physical qubits to detect/correct errors
- doing fault-tolerant computations on encoded qubits
Let's see how this works...using ZX
Quantum Measurements
$|k\rangle\langle k| \propto$
...collapse the quantum state to a fixed one,
depending on the outcome $k \in \{0,1\}$:
Multi-qubit measurements
$k = 0$
$\Rightarrow$
$+1$ eigenspace of $Z \otimes \ldots \otimes Z$
$k = 1$
$\Rightarrow$
$-1$ eigenspace of $Z \otimes \ldots \otimes Z$
$\propto$
Multi-qubit measurements
$X \otimes \ldots \otimes X$ $\leadsto$
Modelling errors
Pauli errors are modelled by introducing X, Y, or Z
flips on edges in a ZX-diagram:
Modelling errors
Detectable errors flip measurement outcomes:
...whereas undetectable errors pass right through:
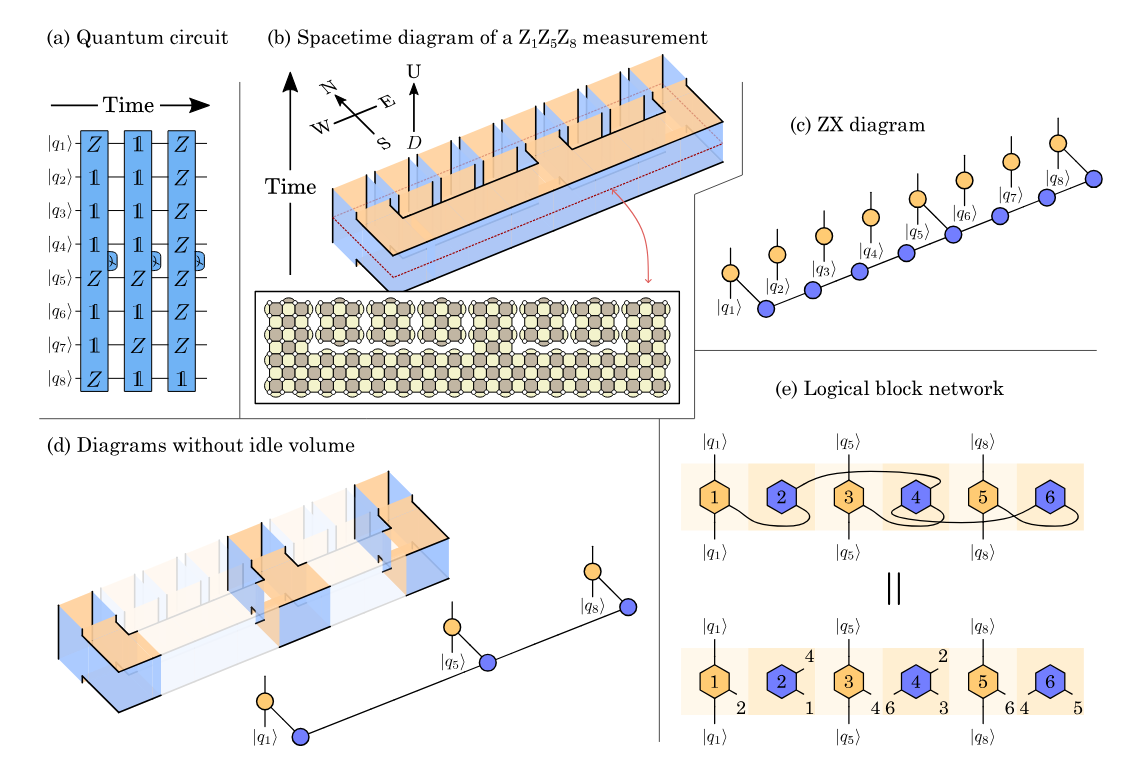
Example: GHZ code
Example: GHZ code
Example: GHZ code
giving an error syndrome.
Graphical encoders
...give us a simple dictionary between QEC codes and ZX-diagrams, e.g. the GHZ code can be fully represented as:
Example: Steane code
Example: Surface code
Example: [[8, 3, 2]] Colour code
Fault-tolerant computation
But codes are only half the story in FTQC. We also need to know how to implement operations fault-tolerantly.
How can we implement this?
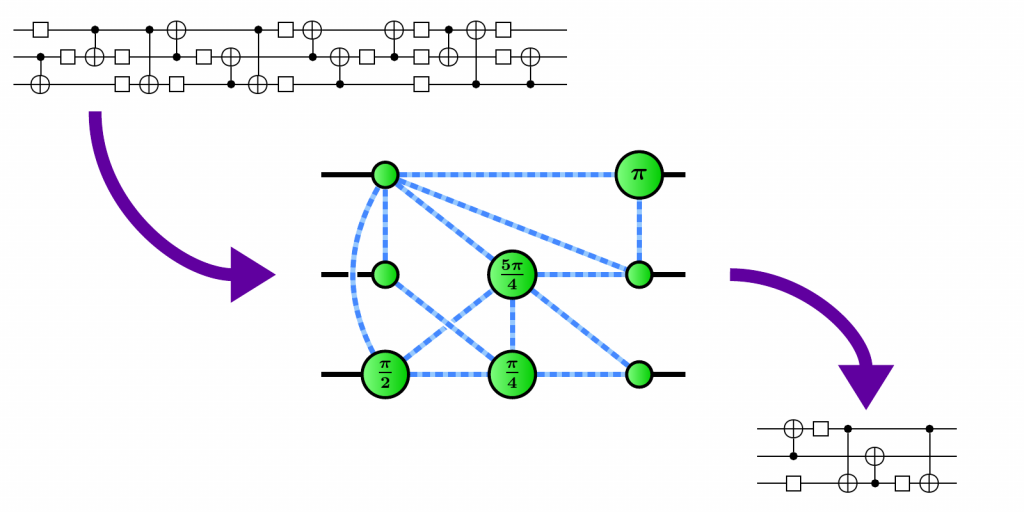
Example: measurement circuits
ZX can give us an answer:
Q: Is the LHS really equivalent to the RHS?
A: It depends on what "equivalent" means.
Example: measurement circuits
They both give the same linear map, i.e. the behave the same in the absence of errors.
But they behave differently in the presence of errors, e.g.
Solution: Fault equivalence
What we need is a notion of equivalence that captures the behaviour of circuits (or ZX-diagrams) in the presence of errors, fault-equivalence:
$D \ \hat{=}\ E$
$D\ \hat{=}\ E \implies D = E$
$D = E \ \ \not\!\!\!\implies D\ \hat{=}\ E$
Fault-equivalence
Definition: Two circuits (or ZX-diagrams) $C, D$ are called fault-equivalent:
$C \ \hat{=}\ D$
"Every undetectable fault in $C$ has a corresponding fault
in $D$ that is $\approx$ as likely."
Fault-equivalence
- While all the ZX rules preserve map-equivalence, only some rules preserve fault-equivalence.
- It turns out the ones that do, e.g.
...are very useful for compiling fault-tolerant circuits!
Paradigm: Fault-tolerance by construction
Idea: start with an idealised computation (i.e. specification) and refine it with fault-equivalent rewrites until it is implementable on hardware.
Specification/refinement has been used in formal methods for classical software dev since the 1970s. Why not for FTQC?
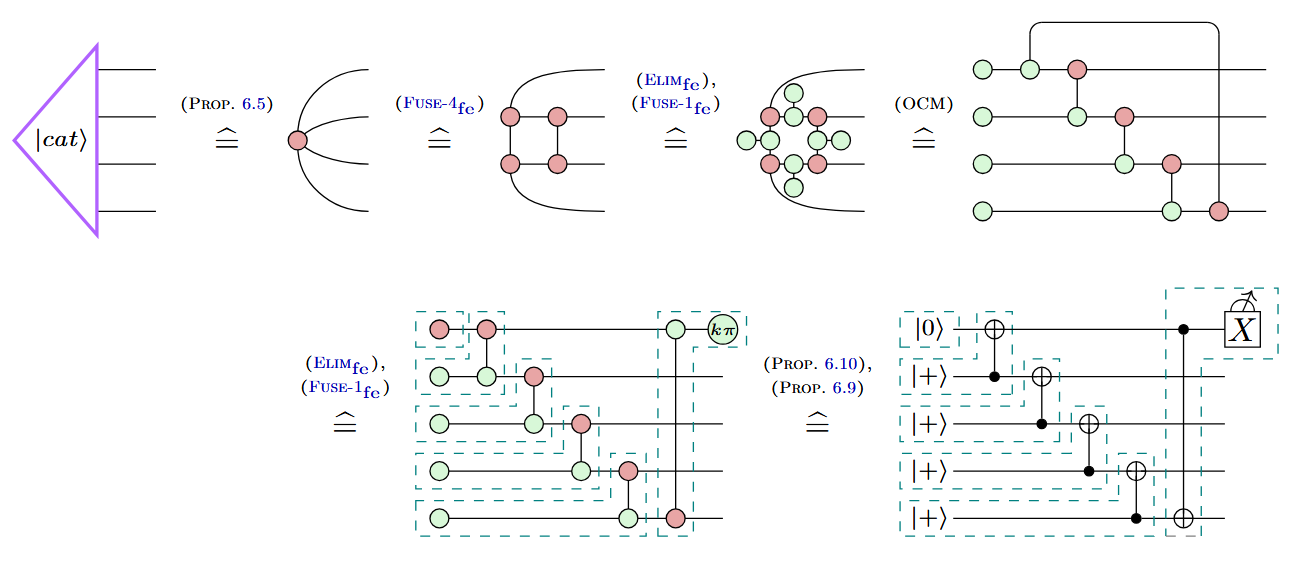
Example: Cat state preparation
Example: Shor-style syndrome extraction
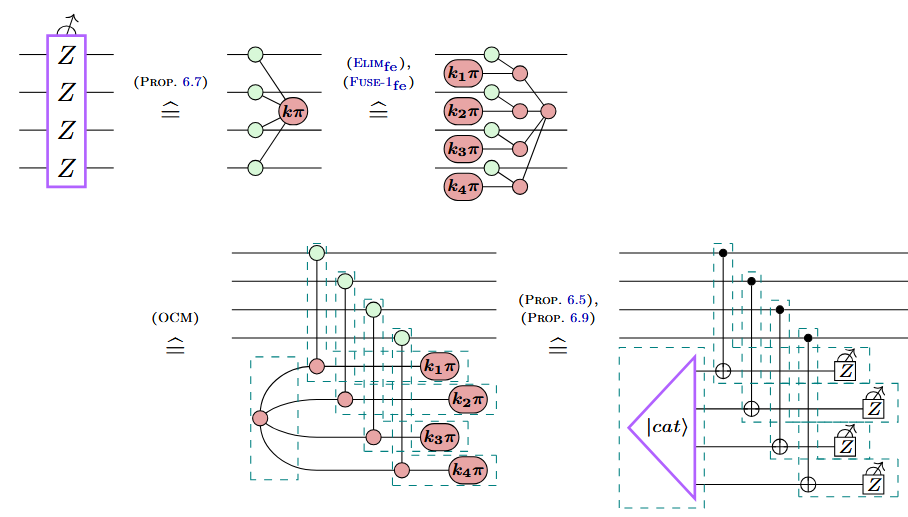
Example: A new variation on Shor
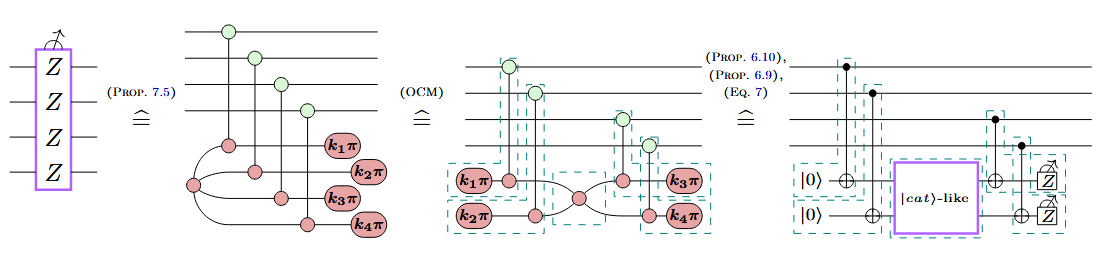
Lots to do!
- Automatically building/optimising FT circuits
(e.g. via heuristic search or AI)
- Logical computation and measurement
(esp. in non-traditional QEC paradigms, like dynamical codes)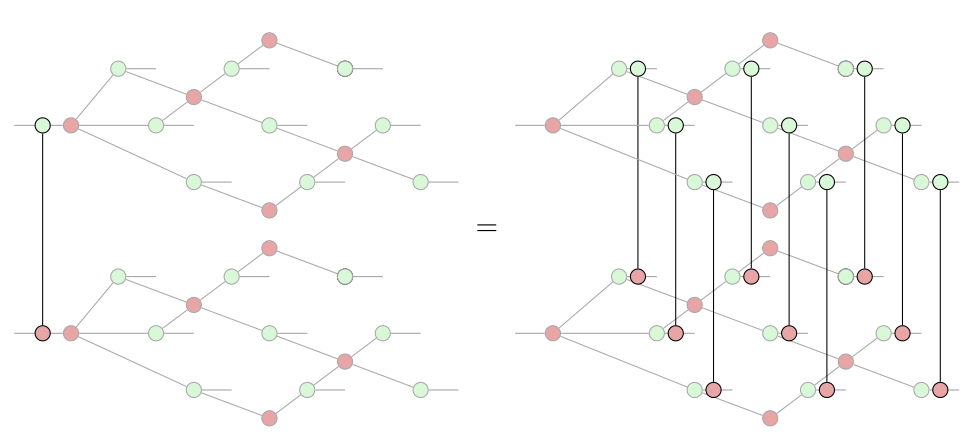
Lots to do!
- Scalability / compositionality
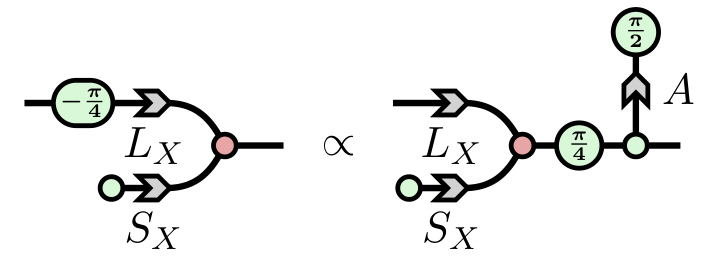
- Tooling, automation, and integration
(PyZX/QuiZX/ZXLive/Stim)
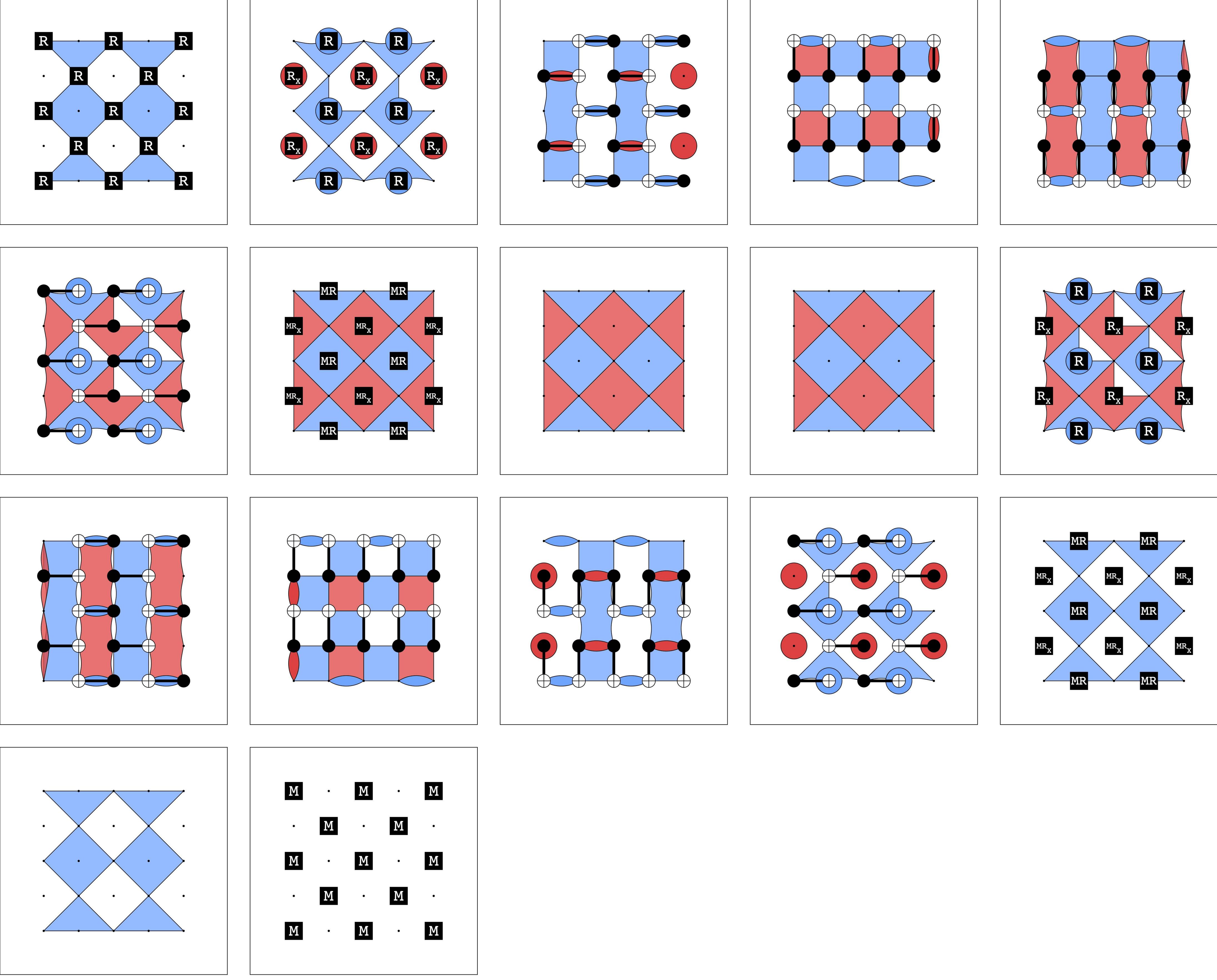
Lots to do!
- Decoding errors and preserving efficient decodability

- Reasoning about stochastic noise
(fault-equiv. = adversarial/worst-case noise behaviour)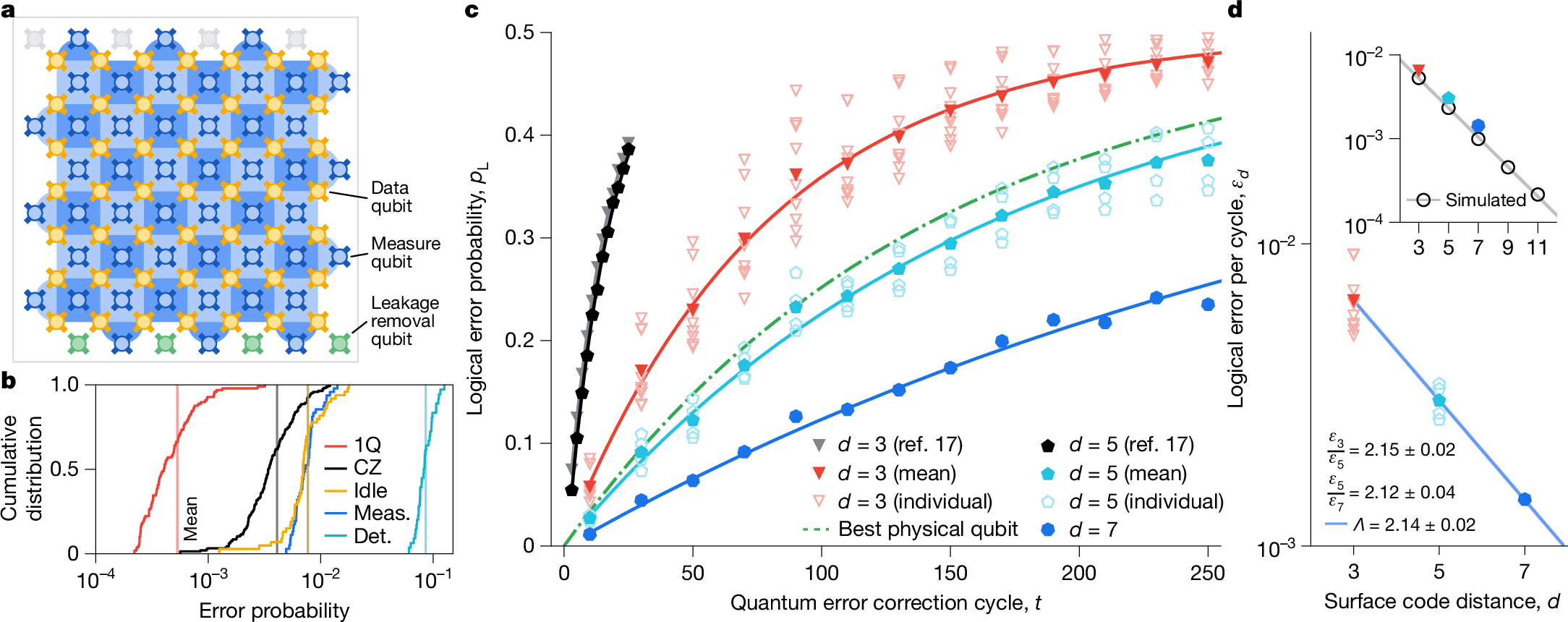
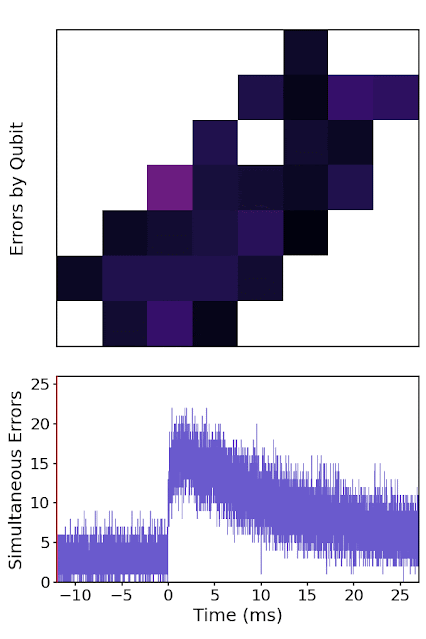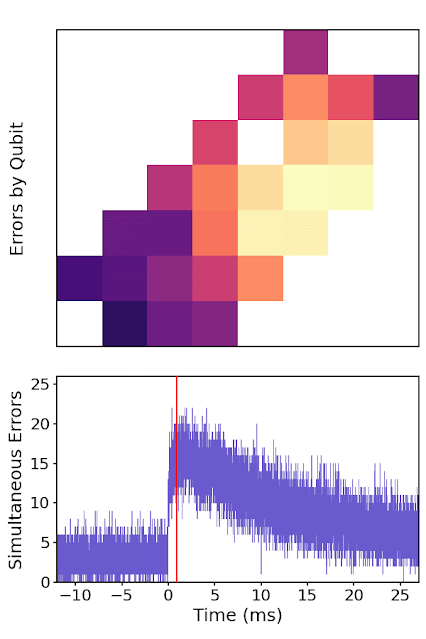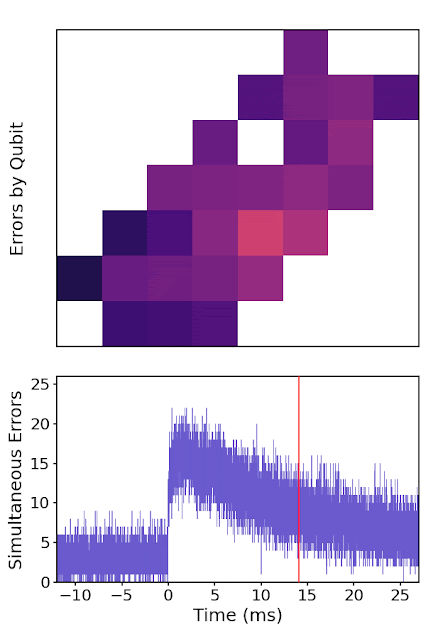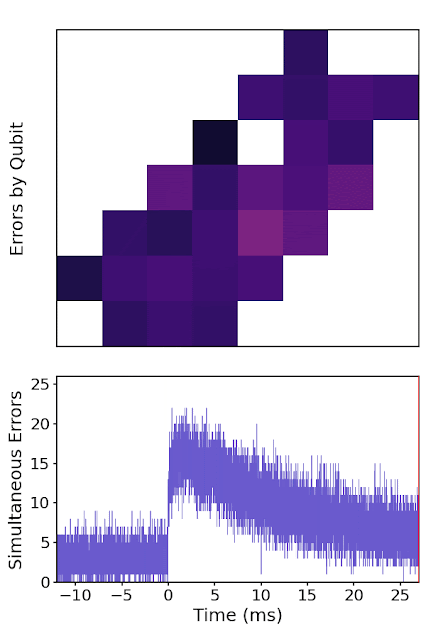
Image credit: Riverlane and Google Quantum AI
Lots to do!
- Biased or hardware-inspired noise


- Finding cool FT protocols, running them on hardware, e.g.


"Fault Tolerance by Construction". Rodatz, Poór, Kissinger
arXiv:2506.17181

https://zxcalc.github.io/book
(free book! Ch 12 = ZX + QEC)
https://zxcalculus.com
(>350 ZX papers, online seminars, Discord)