Picturing Quantum Software
Aleks Kissinger and John van de Wetering
ZX Calculus Seminar 2025


https://zxcalc.github.io/book
Picturing Quantum Software
A new textbook introducing teaching core quantum software/compiling concepts using the language of ZX
 |
 |
 |
| Circuit synthesis & optimisation | Classical simulation | QEC & Fault tolerance |
CH1: Intro
Quantum Software is the code that runs on a quantum computer
|
INIT 5 CNOT 1 0 H 2 Z 3 H 0 H 1 CNOT 4 2 ... |
↔ |
ZX Calculus
- ...is a convenient graphical language for reasoning about quantum software
- E.g. ZX diagrams readily express quantum circuits:
$\textit{CNOT} :=$
$\sqrt{X} :=$
$Z_\alpha :=$
...
- Complete for circuit equality with only a few rules
CH2: Quantum theory is SCUM
- A short (~50 page) intro to quantum theory and the circuit model using the SCUM postulates:
- S. States are vectors
- C. Compound systems are given by tensor product
- U. Unitaries are time evolution
- M. Measurements according to the Born/Lüders rule
-
Honorable mention: tensor networks and Penrose diagrams
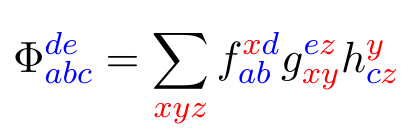
CH3: ZX Basics
- ZX diagrams and rules, with intuition, examples, and exercises
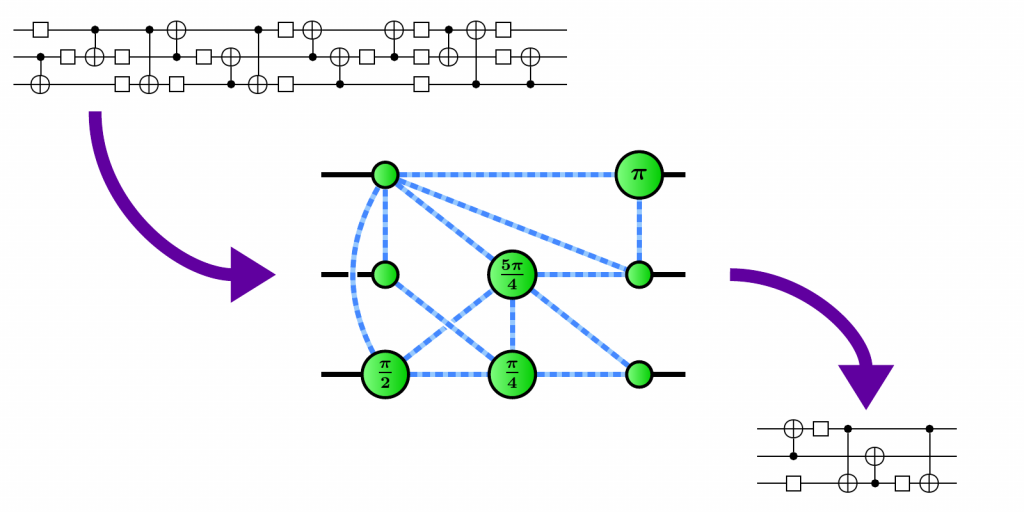
CH4: CNOT Circuits & Phase-free ZX
$\textit{CNOT} :=$
- CNOT circuits correspond to parity maps, which send basis elements to XORs of basis elements
- Using this fact, CNOT circuits can be efficiently represented as $\mathbb F_2$ matrices and synthesised using Gaussian elimination
- The phase-free ZX calculus is very simple:
-
This is complete for phase-free diagrams, and can efficiently reduce those diagrams to generalised parity form:
- When $j = k = 0$, this reduces to Parity Normal Form, which we describe compactly as matrix arrows:
...a preview of scalable notation for ZX diagrams$|\vec x\rangle \ \mapsto \ |A\vec x\rangle$
-
Phase-free rules correspond to $\mathbb F_2$-linear algebra, e.g. strong complementarity is substitution:
This is used to develop techniques used for CNOT circuits (and later for generalised circuits and QEC)
CH5: Clifford Circuits & Diagrams
The Clifford ZX calculus
A complete set of equations for qubit Clifford QC
efficient synthesis, equality checking, & strong classical simulation
- Clifford circuits are built from:
$\textit{CNOT} :=$
$H :=$
$S :=$
- Using Clifford ZX rules, these can efficiently be reduced to normal form
GSLC form AP form
- $\Rightarrow$ Clifford circuit (re)synthesis and normal forms
- $\Rightarrow$ pure-ZX proofs of efficient equality checking and Gottesman-Knill
CH6: Stabiliser Theory
- Multi-qubit Pauli measurements:
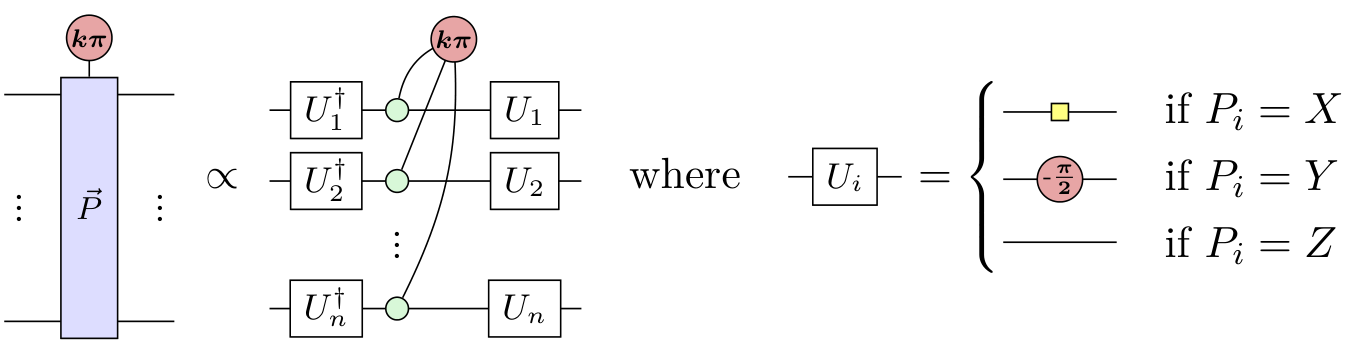
- Proof of the Fundamental Theorem of Stabiliser Theory
- Equivalence of tableau and ZX reps. of stabiliser states/maps
CH7: Universal Circuits
- Efficient representation of CNOT+phase circuits using phase polynomials/phase gadgets:
$=$
- Circuit optimisation via "phase folding"
- Representing/rewrite universal circuits via
- Sum-over-paths (a.k.a. Feynman sums/discrete Feynman integrals)
- Pauli exponentials
- Hamiltonian simulation via Trotterization:
CH8: Interlude (cheatsheets!)
CH9: MBQC and ZX Circuit Extraction
ZX Circuit Optimisation has 2 phases. First simplify...
$\Rightarrow$
...and extract:
Circuit extraction from ZX diagrams is #P-hard in general, but it can be done in poly-time in the presence of generalised flow.
- ZX diagrams as MBQC programs
- Generalised flow (gflow) and determinism
- Polynomial-time circuit extraction using gflow
CH10: Controlled gates and classical oracles
CCZ
$=$
$=$
- Multi-controlled gates, via phase gadgets and H-boxes
- ZH rules and (graphical) Fourier transform
- Classical reversible logic synthesis
- Building arithmetic circuits
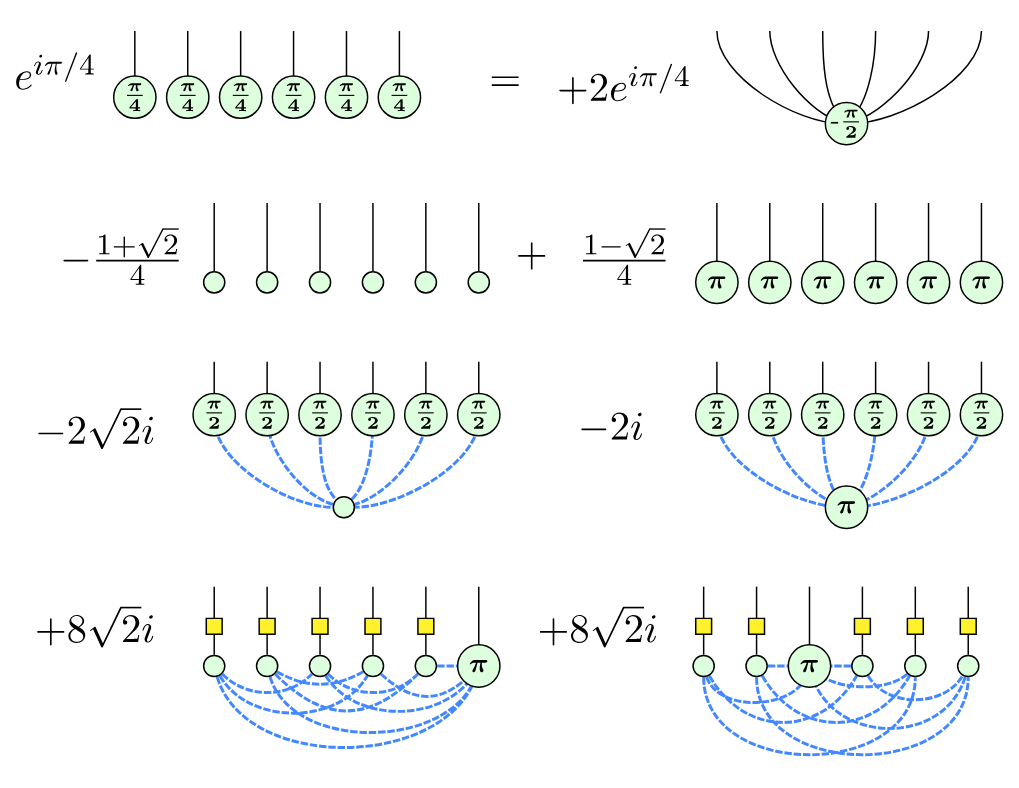
CH11: Clifford+T ZX diagrams
- Universality of Clifford+T, via number theoretic synthesis
$\ =\ \frac{1}{\delta^2} \begin{pmatrix} 1 + \omega - \omega^3 & -1 - \omega - \omega^2 \\ 1 + \omega + \omega^2 & \omega + \omega^2 + \omega^3 \end{pmatrix}$
- Triorthogonality and spider nests
$\Rightarrow$
- T-count optimisation (Reed-Muller & TODD-style)
- Compilation with catalysis
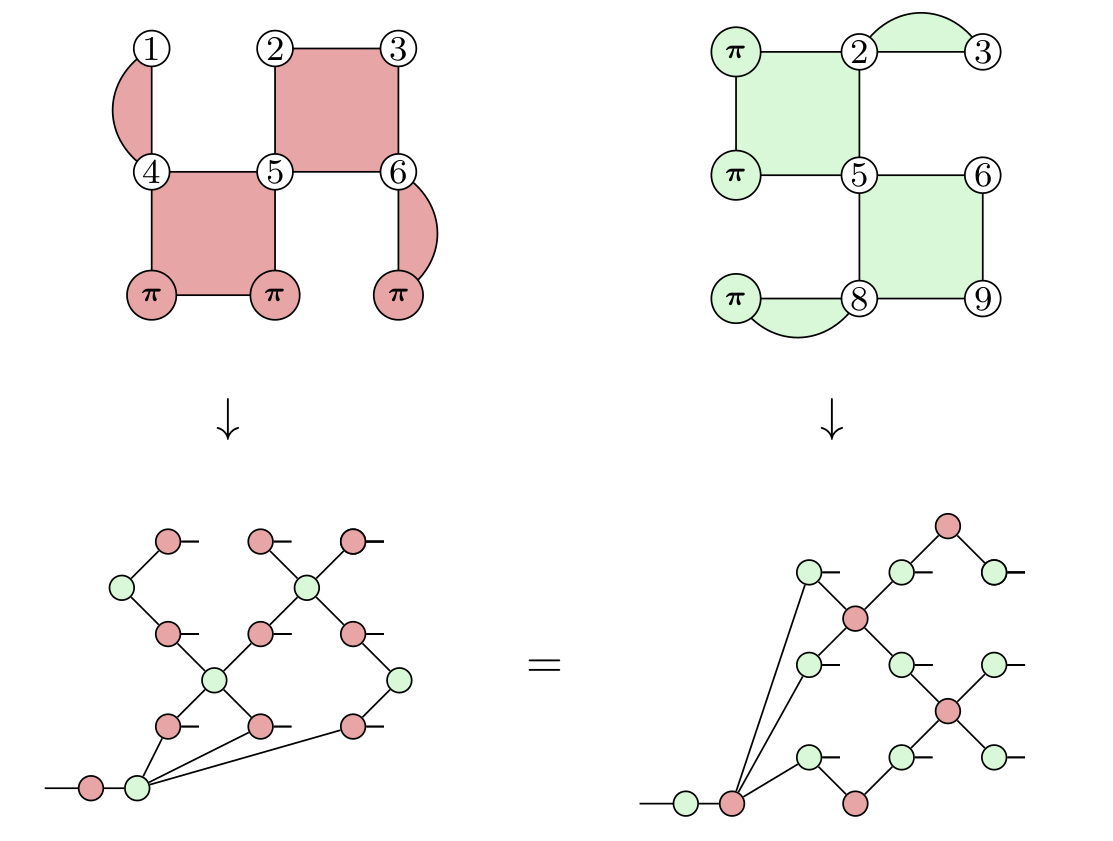
CH12: Quantum Error Correction
into a bigger space of physical qubits:
- $E$ (or just $\textrm{Im}(E)$) is a called a quantum error correcting code
- QECCs are used to:
- encode (and sometimes decode) logical states
- measure physical qubits to detect/correct errors
- do fault-tolerant computations on encoded qubits
- The idea: represent the encoder isometry $E$ directly as a ZX diagram
$\quad = \quad$
- Fault-tolerant QC $:=$ pushing through the encoder
- For CSS codes, this is especially convenient, since the encoders correspond directly to logical/check structure, e.g.
Steane code [[8, 3, 2]] colour code Surface code - We can even work with check matrices directly using scalable notation:
$E \ \ =$
$=$
Application: Transversal Cliffords
Application: transversal non-Cliffords
...when $(L_X, S_X)$ is a triorthogonal code.
Application: lattice surgery
...and a couple more things to mention before we go:
- Fault-tolerant syndrome extraction
- Magic state distillation
Enjoy!

https://zxcalc.github.io/book
If you find a bug, post an issue on GitHub. If you want to teach with this book, we have problem sheets, solutions, and syllubi, so get in touch!