Worksheet 3: Definitions and functions

Remember that rot can be applied twice to a picture to turn it upside down:

rot(rot(man))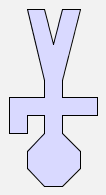

rot(rot(woman))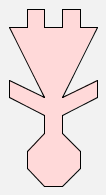

It would be convenient to make a new function that could be used when we want two successive rotations to be applied to a picture, as in the examples above. We can do this using an expression with define, like this:

define rot2(p) = rot(rot(p))

The command define makes the expression that follows it on the left hand side of the = sign to stand for the expression on the right of the = sign.

When you type this definition in place of an expression, GeomLab responds with the message

--- rot2 = <function>

This shows the rot2 has been defined as a function: it is not a picture in itself, but it produces a picture when we supply an argument (i.e., the picture that is to be rotated). Having defined the function rot2, we can use it in the same way as any other function:

rot2(man)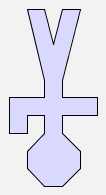

In order to use a defined function in an expression, we just type both the definition and the expression in the input window, like this:

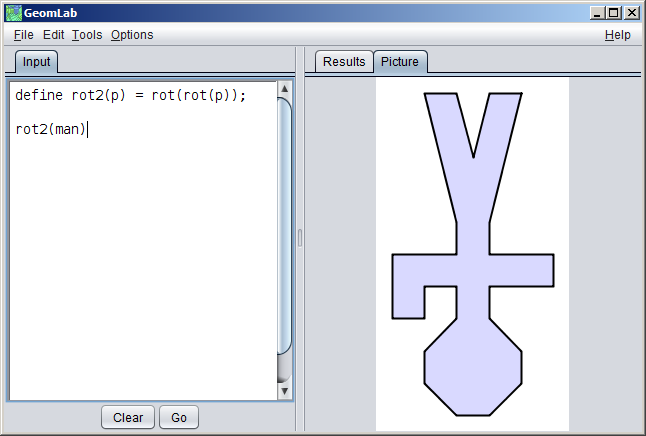
Each definition ends with a semicolon, and that helps GeomLab to keep it separate from the following definition or expression.

Replacing man by tree gives another upside down picture:

rot2(tree)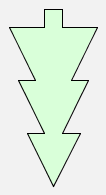

Note that the variable p used in the expression defining rot2 is a placeholder. This means that the function rot2 can be applied to any expression put in place of variable p, such as man or woman.

Let us consider another function definition:

define f(p) = p $ (p & p)

This makes a picture that contains three copies of the argument picture:

f(man)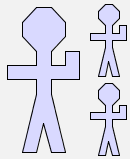

f(woman)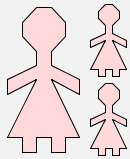

What will the image produced by f(man) $ tree look like? Sketch the picture here:

f(man) $ tree

Check your answer in GeomLab: again, you must enter simultaneously both the definition of f and the expression that uses it.

Here is the image produced by f(man $ tree):

f(man $ tree)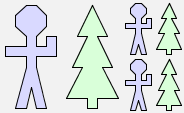

This image is different from the one produced by f(man) $ tree. This is because the brackets in the first example are not around tree, so the function f is applied only to man, whereas the second example has brackets that include tree, so the function f is applied to the expression man $ tree.

f(man $ tree) = (man $ tree) $ ((man $ tree) & (man $ tree))
f(man) $ tree = (man $ (man & man)) $ tree

Now look at the picture f(f(man)):

f(f(man))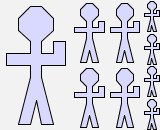

Looking at the picture above, there are nine men produced by applying function f twice to man. What happens if we apply function f three times to man, as in f(f(f(man)))? How many men do you think will be in the picture? Try it!

As described in Worksheet 2, a function takes one or more arguments. For example, the function f that we defined earlier takes one argument, which could be man, woman or any other picture expression.

Let us define a function g that takes two arguments:

define g(p, q) = (p & q) $ (q & p)

Here is what g(man,woman) looks like:

g(man, woman)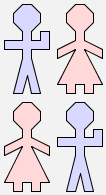

What will happen if we type g(man,g(man,woman)) into GeomLab? Sketch in the space below the image that you think will be produced:

g(man, g(man, woman))

Check your answer in GeomLab.

In this sheet, we have seen how to introduce new functions into the GeomLab language by defining them with a formula that gives their value. This does not increase the variety of pictures that we can describe, for we can always eliminate the new functions from any formula by substituting the defining formula of the function in each place it is used. In essence, this is what the computer does when we ask it to evaluate a formula containing functions we have defined. Although defining functions does not give us new pictures in principle, nevertheless in practice it does let us describe complex pictures much more easily.

In a wider programming context, defining new functions is one of the chief ways programmers keep the complexity of computer systems under control. A good function does a well-defined job, such as solving an equation or displaying a web page, and does it in such a way that you don't need to understand how the function works in order to use it -- just as you don't need to understand how a CD player works in order to play music on it. In this way, programmers constantly enrich the vocabulary of their language, making it possible to give succinct instructions for a wider and wider range of tasks. One of the hallmarks of an experienced programmer is an ability to simplify programs and make them easier to understand by introducing appropriate functions.