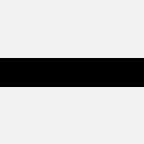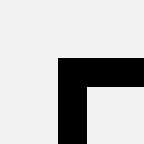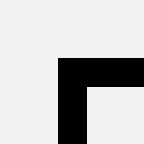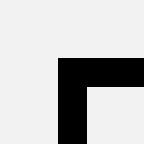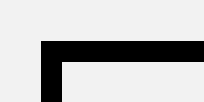Worksheet 5: Spirals and zig-zags

This worksheet uses two constants straight and bend that look like square tiles:

straight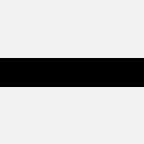

bend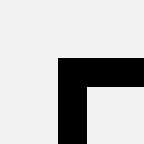

Let's introduce some short names for rotated versions of these basic shapes:

define s = straight
define s1 = rot(s)
define b = bend
define b1 = rot(b)
define b2 = rot(b1)
define b3 = rot(b2)

We can now draw various shapes by putting together the tiles that we have just defined:

define spi1 = b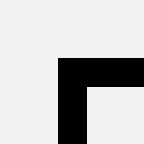

define spi2 = (b $ s) & (b1 $ b2)

define spi3 = (b $ s $ s) & (s1 $ b $ b3) & (b1 $ s $ b2)

The picture for spi4 is shown below on the right. Define spi4 yourself in the space provided, then use GeomLab to test your expression, and see if you are right:

define spi4 =

How can we draw more spirals with more and more turns without typing more and more complicated expressions? The answer is to write a program to do it.

We can start by working out how to draw one arm of a spiral. This is a number of straight's, with a bend at the end. As we did with the rows of men in Worksheet 4, let's begin by drawing the first few sides one at a time, and then look for a pattern:

define a1 = bend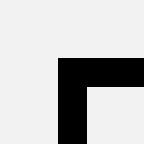

define a2 = bend $ straight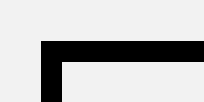

define a3 = bend $ straight $ straight

From the examples above, we can see that we start with a bend and add straight's one at a time. We can express this process using a recursive function, as described in Worksheet 4:

define arm(n) = arm(n-1) $ straight when n > 1
  | arm(1) = bend

The new function arm can now be used to draw sides of desired length:

arm(3)

arm(4)

Let's now try to use our function arm to create some spirals. How can we get from spi2 (defined earlier) to spi3, and from there to the next spiral, and so on? We can see that spi1 is a 2 × 2 arrangement of tiles, and the same tiles appear as one corner of spi3, after being rotated by 180 degrees. The rest of spi3 consists of a rotated copy of arm(2) and a copy of arm(3), as shown in the image below:

arm(3) & (rot(arm(2)) $ rot2(spi2))

(I've separated the parts of the picture a bit, so that you can see how it fits together). The resulting image looks exactly like spi3. This process can be repeated using spi3 to produce spi4, as shown below:

arm(4) & (rot(arm(3)) $ rot2(spi3))

We can see that this process can be applied to any spiral, so it must be possible to use it in a recursive function that draws spirals of any size. Since we have defined spi1 as simply bend, we can use this as a base case for the following recursive definition:

define spiral(n) = ???? when n > 1
  | spiral(1) = bend

Fill in the missing expression in the definition above. Check your answer in GeomLab (type in the completed definition, and try a few examples to see whether the correct picture is produced).

With the completed definition, we can draw spirals with as many turns as we like:

spiral(5)

spiral(10)

(Note: When a complex spiral is drawn, the turns will get very small, and you'll start to see them merge together in a way that may look a bit uneven on the computer screen. Don't worry, this is normal!)

Now here is a challenge for you: define a function zigzag that can draw zig-zags like these:

zigzag(4,3)

zigzag(10,5)

The picture zigzag(m,n) should be m units wide and n units high.

Also, define a function zagzig that can draw shapes like these:

zagzig(5)

zagzig(10)

In this sheet, we have seen more examples of recursive functions that generate a sequence of patterns, each a little more complex than the one before. Each time, the key to finding the proper definition of the function is to work out exactly how a copy of each member of the sequence is embedded in the next member.