NMFcomputations.mws

>   

This sheet performs some computations needed to verify various claims in the paper.

The non-math text in this sheet refers to objects discussed in the paper, e.g., r_1, ..., r_6, P, q_1^*, ...

The sheet is organized in sections that roughly correspond to sections of the paper.

The matrix factorizations claimed in the paper are verified in "Section 4.1 -- Geometry".

>    restart;

>    with(LinearAlgebra):

The following function maps a (nonnegative) matrix to a stochastic (i.e., column-stochastic) one, by normalizing the columns.

>    makeStoch := lA -> Matrix([seq(Normalize(lA[1..RowDimension(lA),i],1), i=1..ColumnDimension(lA))]):

Section 4.1 -- Geometry

The columns of the following matrix are the "inner points" r_1, ..., r_6.

>    InnerPoints := Transpose(Matrix([
[3/4,1/8,0],
[3/4,1/2,0],
[3/11,17/22,0],
[2,0,1/2],
[1/2,0,3/4],
[1/6,0,7/12]]));

InnerPoints := Matrix(%id = 34401844)

The columns of the following matrix contain the vertices of the polyhedron P.

>    OuterPoints := Transpose(Matrix([
[0,0,0],
[1,0,0],
[1,1/2,0],
[0,1,0],
[9/4,0,1/2],
[0,0,8/7]]));

OuterPoints := Matrix(%id = 34500680)

The columns of the following matrix contain the "intermediate points" q_1^*, ..., q_5^*.

>    MediatePoints := Transpose(Matrix([
[2-sqrt(2),0,0],
[(3-sqrt(2))/7,(11+sqrt(2))/14,0],
[1,(3+sqrt(2))/14,0],
[0,0,(10+sqrt(2))/14],
[(26+7*sqrt(2))/17,0,(12-2*sqrt(2))/17]])); evalf(%);

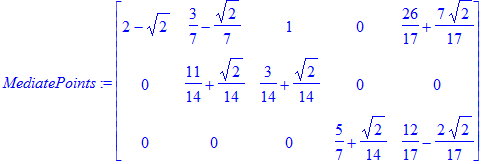
MediatePoints := Matrix(%id = 34525584)

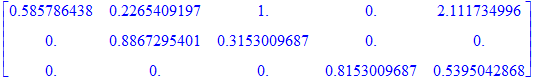
Matrix(%id = 34529812)

>    Hpre := Matrix([
[h11,0  ,h13,h14,0  ,h16],
[0  ,h22,h23,0  ,0  ,0  ],
[h31,h32,0  ,0  ,0  ,0  ],
[0  ,0  ,0  ,0  ,h45,h46],
[0  ,0  ,0  ,h54,h55,0  ]]);

Hpre := Matrix(%id = 34549524)

The following matrix (denoted H below) is the matrix H' from the paper.

>    ({seq(seq(InnerPoints[i,j] = (MediatePoints . Hpre)[i,j], i=1..3), j=1..6)}):
solve(%):
H := subs(%, Hpre);

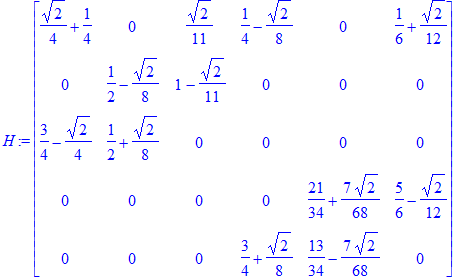
H := Matrix(%id = 36590792)

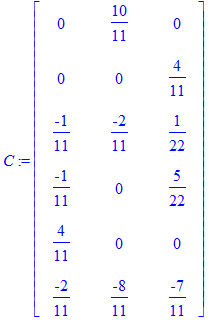
The following matrix is the matrix C.

>    C := Matrix([
[0, 10/11, 0],
[0, 0    , 4/11],
[-1/11, -2/11, 1/22],
[-1/11, 0, 5/22],
[4/11, 0, 0],
[-2/11, -8/11, -7/11]]);

C := Matrix(%id = 36603572)

The following vector is the vector d.

>    d := Vector([0, 0, 2, 1, 0, 8]) / 11;

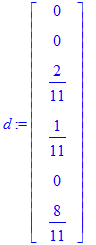
d := Vector(%id = 36631136)

>    Vector[row]([1,1,1,1,1,1]) . C;
Vector[row]([1,1,1,1,1,1]) . d;

Vector(%id = 36706524)

1

The following matrix (denoted M below) is the matrix M' from the paper. We verify that it is stochastic.

>    M := C . InnerPoints + Matrix([d,d,d,d,d,d]); makeStoch(M) - M;

M := Matrix(%id = 34275508)

Matrix(%id = 3490392)

The following matrix is the matrix W. We verify that it is stochastic. We verify that M' = W * H'.

>    W := C . MediatePoints + Matrix([d,d,d,d,d]);  
makeStoch(W)-W, simplify(M - W . H);
evalf(W);

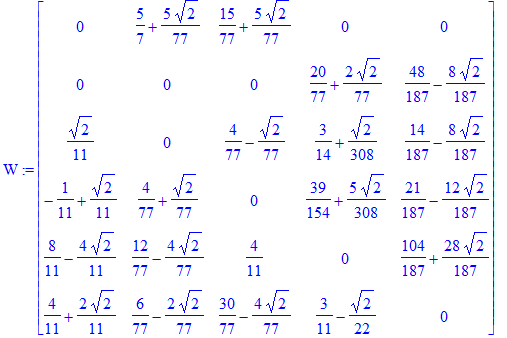
W := Matrix(%id = 3972672)

Matrix(%id = 30724844), Matrix(%id = 30887972)

Matrix(%id = 32764468)

The columns of the following matrix contains the points q_1^epsilon, ..., q_5^epsilon.

>    EpsPoints := Matrix([
[99/169, 121/534, 9337/9338, 1/42216, 813/385],
[0, 133/150, 64/203, 0, 0],
[1/40560, 0, 0, 17209/21108, 997/1848]]);

EpsPoints := Matrix(%id = 36437184)

>    Hepspre := Matrix([
[1-h41-h51,1-h22-h32,1-h23-h33,1-h44-h54,1-h45-h55],
[0  ,h22,h23,0  ,0  ],
[0  ,h32,h33,0  ,0  ],
[h41,0  ,0  ,h44,h45],
[h51,0  ,0  ,h54,h55]
]); Vector[row]([1,1,1,1,1]);

>    EpsPoints - MediatePoints . Hepspre:
seq(seq(%[i,j], j=1..5), i=1..3):
solHeps := solve({%}):

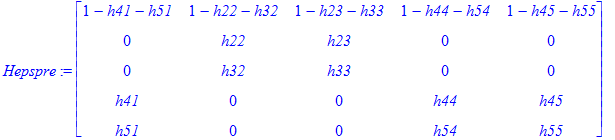
Hepspre := Matrix(%id = 32742220)

Vector(%id = 35691140)

The following matrix is the matrix H_epsilon. We verify that it is stochastic.

>    Heps := subs(solHeps, Hepspre); makeStoch(Heps) - Heps; evalf(Heps);

Heps := Matrix(%id = 3423704)

Matrix(%id = 3459948)

Matrix(%id = 3459996)

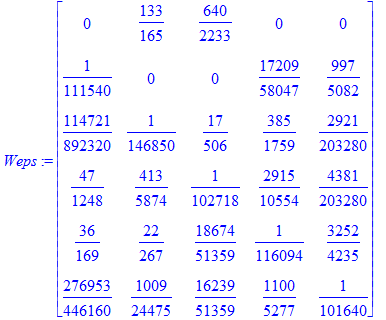
The following matrix is the matrix W_epsilon. We verify that it is stochastic.

>    Weps := C . EpsPoints + Matrix([d,d,d,d,d]);
makeStoch(Weps) - Weps;
evalf(Weps);

Weps := Matrix(%id = 3795732)

Matrix(%id = 30580860)

Matrix(%id = 35394820)

We verify that W_epsilon = W * H_epsilon.

>    simplify(Weps - W . Heps);

Matrix(%id = 30609804)

Section 4.2 -- Type 1

In the following we perform determinant computations pertaining to the polygon P_0 (type-1 case).

>    Matrix([[u,0,1],[1,v/2,1],[3/4,1/8,1]]); det1 := Determinant(%);
Matrix([[1, v/2, 1], [1-w, 1/2 + w/2, 1], [3/4, 1/2, 1]]); det2 := Determinant(%);
Matrix([[1-w, 1/2 + w/2, 1], [u, 0, 1], [3/11, 17/22, 1]]); det3 := Determinant(%);
eliminate({det1, det2}, {v, w}); f := simplify(subs([%[1]][1], det3)); solve(%);

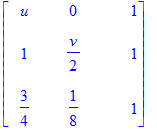
Matrix(%id = 32440644)

det1 := 1/2*u*v-1/8*u+1/8-3/8*v

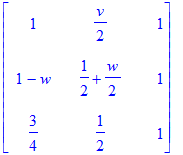
Matrix(%id = 36156028)

det2 := -3/8*w+1/8-1/8*v+1/2*w*v

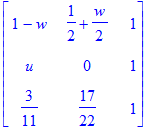
Matrix(%id = 32508624)

det3 := -7/11+10/11*w+3/11*u-1/2*u*w

[{v = (u-1)/(4*u-3), w = (3*u-2)/(8*u-5)}, {}]

f := 15/22*(-4*u+2+u^2)/(8*u-5)

2+2^(1/2), 2-2^(1/2)

>    plot(f, u=0..0.6);

[Maple Plot]

In the following we perform determinant computations pertaining to the polygon P_1 (type-1 case).

>    Matrix([[u,0,1], [(9-9*v)/4, (7+9*v)/14, 1], [2, 1/2, 1]]); det1 := Determinant(%);
Matrix([[(9-9*v)/4, (7+9*v)/14, 1], [0, (8-8*w)/7, 1], [1/2, 3/4, 1]]); det2 := Determinant(%);
Matrix([[(0,8-8*w)/7, 1], [u, 0, 1], [1/6, 7/12, 1]]); det3 := Determinant(%);
eliminate({det1, det2}, {v,w}); f := simplify(subs([%[1]][1], det3)); solve(%);

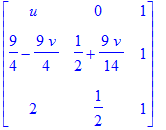
Matrix(%id = 35258392)

det1 := 9/14*u*v+1/8-135/56*v

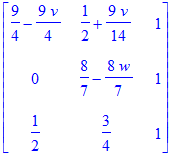
Matrix(%id = 33184452)

det2 := 9/16-2*w-9/16*v+18/7*w*v

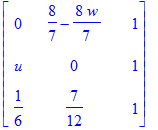
Matrix(%id = 33288720)

det3 := 4/21-47/84*u+8/7*u*w-4/21*w

[{w = 1/16*(9*u-32)/(2*u-7), v = -7/9/(4*u-15)}, {}]

f := -10/21*(-4*u+2+u^2)/(2*u-7)

2-2^(1/2), 2+2^(1/2)

>    plot(f, u=0.5..1);

[Maple Plot]

Section 4.5 -- Type 4

The following functions up and lo round up and down to n decimal digits.

>    up := (x,n) -> evalf(ceil(x*10^n)/10^n):
lo := (x,n) -> evalf(floor(x*10^n)/10^n):

>    up(0.123456,3); lo(0.123456,3);

.1240000000

.1230000000

In the following we verify computations of bounds for the type-4 case.

>    W12lo := lo(W[1,2],2);

W12lo := .8000000000

>    W13lo := lo(W[1,3],3);

W13lo := .2860000000

>    W13up := up(W[1,3],3);

W13up := .2870000000

>    W24lo := lo(W[2,4],2);

W24lo := .2900000000

>    W25lo := lo(W[2,5],3);

W25lo := .1960000000

>    W33lo := lo(W[3,3],4);

W33lo := .3350000000e-1

>    W34lo := lo(W[3,4],2);

W34lo := .2100000000

>    W35up := up(W[3,5],3);

W35up := .1500000000e-1

>    W42lo := lo(W[4,2],3);

W42lo := .7000000000e-1

>    W44lo := lo(W[4,4],2);

W44lo := .2700000000

>    W45up := up(W[4,5],3);

W45up := .2200000000e-1

>    W55lo := lo(W[5,5],3);

W55lo := .7670000000

>    W61lo := lo(W[6,1],2);

W61lo := .6200000000

>    W63up := up(W[6,3],2);

W63up := .3200000000

>    W64up := up(W[6,4],2);

W64up := .2100000000

>    ex := 5;
eps := 10.^(-ex);

ex := 5

eps := .1000000000e-4

>    R24lo := W24lo;

R24lo := .2900000000

>    R25lo := W25lo;

R25lo := .1960000000

>    L32up := up(W35up/R25lo,3);

L32up := .7700000000e-1

>    L42up := up(W45up/R25lo,2);

L42up := .1200000000

>    L62up := up(eps/R25lo,ex);

L62up := .6000000000e-4

>    L52up := up(eps/R24lo,ex);

L52up := .4000000000e-4

>    L22lo := lo(1 - L32up - L42up - L52up - L62up,2);

L22lo := .8000000000

>    R21up := up(eps/L22lo,ex);

R21up := .2000000000e-4

>    L63lo := lo(W61lo - L62up*R21up,2);

L63lo := .6100000000

>    L54lo := lo((W55lo - L52up)/(1-R25lo),4);

L54lo := .9539000000

>    L34up := 1 - L54lo;

L34up := .461000000e-1

>    2*L32up, 2-3*L63lo, 2*L34up;

.1540000000, .170000000, .922000000e-1

>    L35lo := lo( (2*W34lo - W64up - max(2*L32up, 2-3*L63lo, 2*L34up))/2, 3);

L35lo := .2000000000e-1

>    L44up := 1 - L54lo;

L44up := .461000000e-1

>    2*L42up, 2 - 3*L63lo, 2*L44up;

.2400000000, .170000000, .922000000e-1

>    L45lo := lo((2*W44lo - W64up - max(2*L42up, 2 - 3*L63lo, 2*L44up))/2,3);

L45lo := .4500000000e-1

>    L11lo := W12lo;

L11lo := .8000000000

>    R12lo := W12lo;

R12lo := .8000000000

>    R13lo := W13lo;

R13lo := .2860000000

>    L31up := up(eps/R12lo,ex);

L31up := .2000000000e-4

>    R13up := up(W13up/L11lo,2);

R13up := .3600000000

>    R33up := up(W63up/L63lo,2);

R33up := .5300000000

>    R53up := up(eps/L45lo,ex);

R53up := .2300000000e-3

>    R43lo := lo(1 - R13up - R33up - R53up,2);

R43lo := .1000000000

>    L44up := up(eps/R43lo,ex);

L44up := .1000000000e-3

>    L41up := up(eps/R13lo,ex);

L41up := .4000000000e-4

>    R52up := up(eps/L35lo,ex);

R52up := .5000000000e-3

>    L43lo := lo( (W42lo - L41up - L44up - R52up) / (1-R12lo), 3);

L43lo := .3460000000

>    maxlo := lo( (W33lo - L31up - R53up) / (1-R13lo), 4);

maxlo := .4650000000e-1

>    is(maxlo + L43lo + L63lo > 1);

true

>    is(maxlo + L54lo > 1);

true

>