Pseudospectra have been independently invented at least five times,
as summarized in the table below.
For further information, see [Tre99b].
| author |
year |
terminology |
motivation
|
| Henry Landau |
1974 |
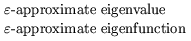 |
Landau studied the asymptotic spectra of non-Hermitian integral operators
(and, implicitly, the associated Toeplitz matrix eigenvalue problem)
[Lan75]. He later applied these ideas to integral
operators that arise in the study of unstable resonators
[Lan76] and lasers
[Lan77].
|
| Jim Varah |
1977 |
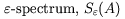 |
Varah was interested in the stability of invariant subspaces of matrices
in the context of numerical solution of non-Hermitian
eigenvalue problems
[Var79].
|
Sergei Godunov,
Novosibirsk Group |
1980s |
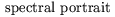 |
This research was primarily directed towards developing techniques for
guaranteed-accuracy eigenvalue computations
[GKK90],
[KR85].
|
| Nick Trefethen |
1988 |
 |
This work had its roots in observations concerning unstable
eigenvalues of spectral discretization matrices for differential
equations. The first published work concerned polynomial iterative methods
for solving systems of linear algebraic equations
[Tre90]
and spectral methods
[RT90].
|
Diederich Hinrichsen,
Tony Pritchard |
1990 |
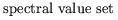 |
Hinrichsen and Pritchard originally studied spectral value sets
in control theory [HP92].
In this context, they have been especially interested
in structured perturbations of a matrix.
In the mid-1980s, they began studying "stability radii",
a closely related quantity measuring the distance to instability
under specific perturbations.
|
Other early uses of pseudospectra include
Wilkinson and
Demmel [Dem87a],
who apparently followed the definitions of
Varah [Var79],
and Chatelin, who apparently followed Godunov.
|

