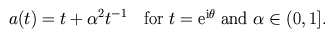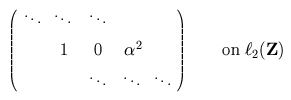Pseudospectra of Random Matrices:
Tridiagonal Toeplitz Matrices with Random Impurities
Consider tridiagonal Toeplitz and Laurent operators determined by
the symbol
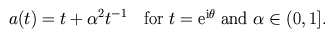
These operators can be considered as infinite matrices.
In the Laurent case, we have
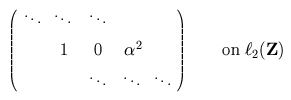
and in the Toeplitz case, we have
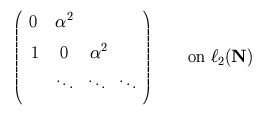
The spectrum of the Laurent operator is the ellipse a(ei theta),
while the spectrum of the Toeplitz operator is the same ellipse together
with its interior.
Suppose now that we add a real perturbation of magnitude no larger
than epsilon to a single entry of the infinite dimensional
matrix. How does the spectrum change over all such perturbations?
Perturbations at each site lead to "antennae" that extend from the
ellipse. The figures below illustrate the union of all such antennae,
and numerical computations show that this phenomenon is realized
for finite dimensional problems.
When alpha=1 , this is
connected to observations of Gilbert Strang and his students in
their studies of small world networks.
When the perturbation is restricted to the diagonal,
this spectrum has been proposed by Feinberg and Zee [2] as
a "single impurity" model in non-Hermitian quantum mechanics.

|
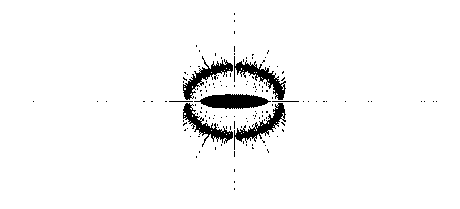
Figure 1. Union over all possible real single site perturbations
(except in the first subdiagonal)
of magnitude 5 for the Laurent operator with alpha=0.4.
Perturbations of this magnitude to the first subdiagonal would
fill in the interior of the ellipse.
|

|
Figure 2. Computed eigenvalues of 1000 circulant matrices (with alpha=0.4)
of dimension 50, each perturbed in a single random entry by a random number uniformly
distributed in [-5,5].
|

|
Figure 3. Union over all possible real single site perturbations
of magnitude 5 for the Toeplitz operator with alpha=0.4.
|
|