Pseudospectra of a Spectral Approximation of an Orr-Sommerfeld Operator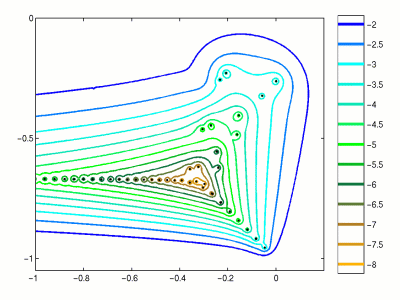

This figure illustrates pseudospectra of an Orr-Sommerfeld operator generated from a spectral method. This discretization results in a matrix of dimension N=99. There are numerous spurious eigenvalues beyond the plotted axis, so the matrix is projected onto an appropriate invariant subspace to accelerate the computation. Pseudospectra of Orr-Sommerfeld operators were first investigated by Reddy, Schmidt, and Henningson [RSH93].

Use the following MATLAB code compute a similar image using EigTool.

  R = 5772;
  N = 100;
  [D,x] = cheb(N);     % cheb.m from Trefethen's "Spectral Methods in MATLAB"
  D2 = D^2; D2 = D2(2:N,2:N);
  S = diag([0; 1 ./(1-x(2:N).^2); 0]);
  D4 = (diag(1-x.^2)*D^4 - 8*diag(x)*D^3 - 12*D^2)*S;
  D4 = D4(2:N,2:N);
  I = eye(N-1);
  A = (D4-2*D2+I)/R - 2i*I - 1i*diag(1-x(2:N).^2)*(D2-I);
  B = D2-I;
  C = B\A;
  opts.npts=50;
  opts.ax = [-1 .2 -1.05 0];
  opts.levels = -10:.5:-2;
  opts.proj_lev = 1;
  eigtool(C,opts)