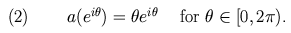Pseudospectra of Toeplitz Matrices and Operators:
Matrices with Piecewise Continuous Symbols
Recall that the entries of a Toeplitz matrix are the Laurent coefficients
of a function known as the symbol, whose domain is the unit circle.
If a Toeplitz matrix is banded, then the symbol is a trigonometric polynomial,
and the resolvent norm of the finite dimensional operator grows exponentially
at points within the spectrum of the corresponding infinite dimensional operator.
The pseudospectra of finite dimensional Toeplitz matrices converge to those
of the infinite dimensional operator, and this convergence is extremely rapid
(exponential in the matrix dimension).
For examples, see the page of banded Toeplitz examples.
Böttcher proved that the pseudospectra of the finite dimensional Toeplitz
matrices must converge to the pseudospectra of the infinite dimensional operator
even when the symbol is only piecewise continuous [Böt94].
This class of functions is much broader than the trigonometric polynomials
described above.
Do the pseudospectra still converge rapidly to their infinite dimensional
Limits when a discontinuity is present? The answer is no,
in a sense made precise in [BET00].
The examples below, which should be contrasted with the
banded Toeplitz examples,
illustrate this slow convergence.
Our first example arises from the symbol
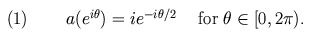 The entries of the Toeplitz matrix determined by (1) are
The entries of the Toeplitz matrix determined by (1) are
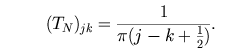 The spectrum of the corresponding infinite dimensional
Toeplitz operator is the right half of the closed unit disk.
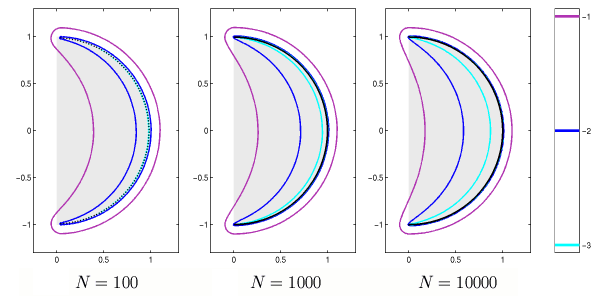
As seen from the plots in Figure 1, the pseudospectra are
far from the unit disk even for relatively large values of
epsilon and large matrix dimensions.
The spectrum of the corresponding infinite dimensional
Toeplitz operator is the right half of the closed unit disk.
As seen from the plots in Figure 1, the pseudospectra are
far from the unit disk even for relatively large values of
epsilon and large matrix dimensions.
This example is related to the "Moler phenomenon", described
in Section 4.5 of [BS99].
The very slow growth of the resolvent norm at z=0
for this example (logarithmic in the matrix dimension)
was established by Tyrtyshnikov [Tyr92].
|
Figure 1. Spectrum and epsilon-pseudospectra
for Toeplitz matrices of dimensions
N=100,
N=1000, and
N=10000
corresponding to the symbol (1).
The symbol of the infinite dimensional operator is the right half
of the unit disk, shaded gray.
A fast Toeplitz algorithm was used to calculate the N=10000 data,
and computations were performed on an SGI Cray Origin2000
at the Oxford Supercomputing Center.
|
Our second example shows similarly slow growth of the pseudospectra for
matrices associated with the symbol
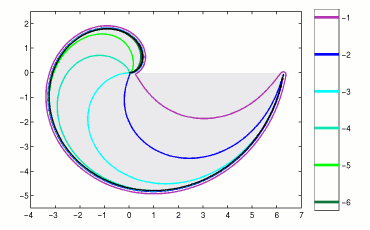
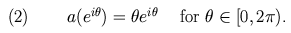 The pseudospectra for three matrices defined by (2) are shown in Figure 2.
The pseudospectra for three matrices defined by (2) are shown in Figure 2.
The limiting behavior of the eigenvalues of the finite dimensional
Toeplitz matrices associated with (1) and (2) has been investigated
by Basor and Morrison [BM94].
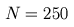 
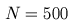 
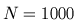 
|
Figure 2. Spectrum and epsilon-pseudospectra
for Toeplitz matrices of dimensions
N=250,
N=500, and
N=1000
corresponding to the symbol (2).
The gray filled region is the spectrum of the infinite dimensional operator.
|
Supplemental Bibliography
References to works included in the
Pseudospectra Bibliography
are presented as links above, and are not repeated here.
| [BM94] |
E. L. Basor and K. E. Morrison
The Fisher-Hartwig conjecture and Toeplitz eigenvalues
Linear Algebra Appl. 202 (1994), 129-142.
MR 95g:47037
|
| [Tyr92] |
E. E. Tyrtyshnikov
Singular values of Cauchy-Toeplitz matrices
Linear Algebra Appl. 151 (1992), 99-116.
MR 92m:47056
|
|