Non standard mathematical approaches for capturing variability
Mathematical modelling in Computational Cardiac Electrophysiology has a long history of over 50 years and can be broadly characterized by the modeling of ion flux dynamics in single cells, coupled, where appropriate, with models for the propagation of an action potential in tissue. The traditional approaches to this have been via ordinary differential equations and partial differential equations, based on the reaction diffusion equation, respectively. In the case of whole heart modeling the implementations often make use of high performance computing. Furthermore, these cell models are often highly tuned. These features of models being highly tuned and deterministic mean that it is very difficult to capture the underlying variability manifested by experiments and additionally that it is impossible to capture the stochasticity that is evident in all biological processes and that occurs at many different spatial and temporal scales.
This strand of work attempts to underpin, using novel mathematical and computer software approaches, the other lines of research in the group.
- In particular it addresses the fundamental question of how to capture the variability through new paradigms such as populations of models calibrated against ranges of experimental data, rather than just the metric of the mean value?
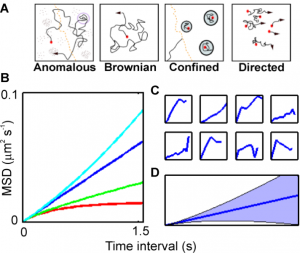
- It also asks how we can build mathematical models that capture ion flux dynamics occurring at the cellular level in terms of the mathematical framework of stochastic differential equations and how these models can be implemented efficiently and to ensure biologically realistic solutions.
- We also attempt to understand the relationship between spatial heterogeneity and cardiac function via modelling. The spatial complexity and heterogeneity of biological tissue can fundamentally alter the laws of standard diffusion and so we ask how can we build novel mathematical models that can capture this heterogeneity in insightful ways?
- This leads to the idea of fractional diffusion models. As these models are nonlocal we then ask how can we build efficient computational techniques to simulate them and how can we validate this nonlocal dynamics?
- Finally, we note that many different types of excitable cells produce an action potential and we ask how we can extend these ideas to other types of excitable cells such as pancreatic Beta cells?
