author	year	terminology	motivation
Henry Landau	1974		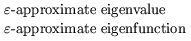Landau studied the asymptotic spectra of non-Hermitian integral operators (and, implicitly, the associated Toeplitz matrix eigenvalue problem) [Lan75]. He later applied these ideas to integral operators that arise in the study of unstable resonators [Lan76] and lasers [Lan77].
Jim Varah	1977		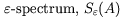Varah was interested in the stability of invariant subspaces of matrices in the context of numerical solution of non-Hermitian eigenvalue problems [Var79].
Sergei Godunov, Novosibirsk Group	1980s		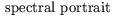This research was primarily directed towards developing techniques for guaranteed-accuracy eigenvalue computations [GKK90], [KR85].
Nick Trefethen	1988		This work had its roots in observations concerning unstable eigenvalues of spectral discretization matrices for differential equations. The first published work concerned polynomial iterative methods for solving systems of linear algebraic equations [Tre90] and spectral methods [RT90].
Diederich Hinrichsen, Tony Pritchard	1990		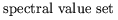Hinrichsen and Pritchard originally studied spectral value sets in control theory [HP92]. In this context, they have been especially interested in structured perturbations of a matrix. In the mid-1980s, they began studying "stability radii", a closely related quantity measuring the distance to instability under specific perturbations.

Other early uses of pseudospectra include Wilkinson and Demmel [Dem87a], who apparently followed the definitions of Varah [Var79], and Chatelin, who apparently followed Godunov.