
Home | Introduction | Software | Examples | History | People | Bibliography | Applications | Theorems

A Brief Survey of Computational MethodsA catalog of software, including the EigTool for MATLAB, is included further down this page. Though pseudospectra were defined theoretically as early as 1975, the first published numerical computation appeared in 1987 [Dem87a] - a 3-by-3 matrix. By 1993, extensive computations involving matrices of dimension 64 were being applied to investigate the behavior of differential operators of fluid mechanics [RSH93]. By 2000, examples of dimensions in the hundreds of thousands had been computed [WT01]. Techniques for the computation of pseudospectra have advanced greatly over the past five years. Almost all efforts have been directed towards computing the 2-norm pseudospectra, which can be characterized in terms of the minimum singular value of zI-A, 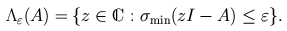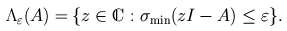
Most algorithms fall into two two broad classes:
Grid algorithms, which are the standard methods, face several challenges. One must first choose a region of the complex plane to investigate, and then very many grid points may be necessary to resolve the desired pseudospectral contours adequately. See [BMT97] for a discussion of the first difficulty and [KG02] for a technique to eliminate some of the uninteresting grid points quickly. Another approach to this latter problem was suggested by Gallestey, whose "SH algorithm" uses the sub-harmonicity of the resolvent norm to recursively eliminate portions of the computational domain [Gal98]. Path-following algorithms also have limitations. One must first find a point on the desired contour; if the pseudospectrum is disconnected, each component must be found; and multiple runs are required if one seeks pseudospectra for several different values of epsilon. Both kinds of algorithm require evaluation of the minimum singular value of zI-A for many different values of z. Considerable progress has been made in making this process as efficient as possible. When A is a dense matrix, Lui noted the advantage of first reducing A to Hessenberg or triangular form before computing the minimum singular value of zI-A [Lui97]. An iterative method can then be used to compute the minimum singular value. Using inverse iteration or inverse Lanczos iteration to compute the minimum singular value seems to be worthwhile for all but the smallest dense matrices, and is essential if A has sparse structure that must be preserved; see also [BH96]. Another speedup technique, which can be applied independently of others, has proved crucial in some applications. When A is large and one only seeks the pseudospectra in a portion of the complex plane, it may be advantageous to project A orthogonally onto a suitably chosen subspace to reduce the problem dimension; see [Lui97], [RSH93], [TT96], [WT01]. For a more detailed tutorial survey of computational techniques for matrices of dimension N<1000, see [Tre99a], where it is claimed that combining various speedups can often accelerate the naive SVD grid algorithm for computing pseudospectra by a factor of about N/4. For larger matrices of dimension up to 106, see [WT01]. The table below lists several different publicly available grid algorithms. At the present, we are unaware of any public domain path-following code for computing pseudospectra. Such software would be a welcome addition. Publicly Available Pseudospectra Software
|