Pseudospectra of a Non-Hermitian Anderson Model
Dimension N=1000

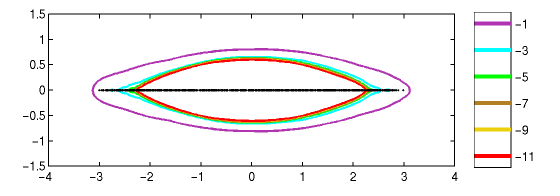
This example of a Non-Hermitian Anderson model is a tridiagonal matrix with has exp(0.4) on the first super-diagonal, exp(-0.4) on the first sub-diagonal, and random entries uniformly distributed between [-1.5,1.5] on the main diagonal. This type of model was first suggested by N. Hatano and D. R. Nelson, "Localization transitions in non-Hermitian quantum mechanics", Phys. Rev. Lett. 77 (1996), 570-573. Pseudospectra of a related random bidiagonal model are analyzed in [TCE01].

Further details about this example can be found on the page:
Pseudospectra of Random Matrices: The Non-Hermitian Anderson Model.

Use the following MATLAB code compute a similar image using EigTool. To mimic the example above, set N=1000 below.

   N = 100;
   g = 0.4;
   A = exp(-g)*diag(ones(N-1,1),-1) + ...
         diag(3*rand(N,1)-1.5) + ...
         exp(g)*diag(ones(N-1,1),1);
   opts.npts = 20;
   opts.ax = [-4 4 -1.5 1.5];
   opts.levels = [-11:-1];
   eigtool(A, opts)