Pseudospectra of a Spectral Approximation of the First Derivative
Dimension N=17

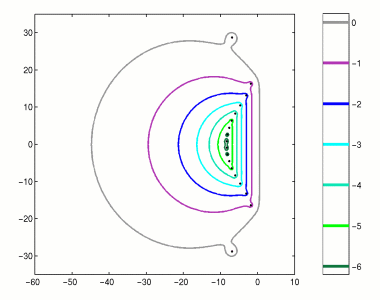
This figure illustrates approximate pseudospectra of the first derivative operator d/dx on [-1,1] with boundary condition u(1)=0. The pseudospectra of the infinite dimensional operator consist of half-planes. This is suggested in this low-dimensional discretization by the straight lines that form the rightmost part of each pseudospectral boundary. For more information, see [Tre92].

Use the following MATLAB code compute a similar image using EigTool.

  [D,x] = cheb(18);       % cheb.m from Trefethen's "Spectral Methods in MATLAB"
  A = D(2:end,2:end);
  opts.npts=50;
  opts.ax = [-60 10 -35 35];
  opts.levels = -6:0;
  eigtool(A,opts)