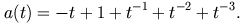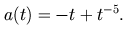Pseudospectra of Toeplitz Matrices and Operators:
Banded Matrices
Banded Toeplitz matrices arise in many applications,
such as the finite difference discretizations of differential equations.
One may wish to know the eigenvalues of such a matrix, for example,
to determine whether the discretization of an initial-boundary value
problem is stable.
Suppose the Toeplitz matrix T is defined entrywise,
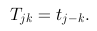
The coefficients tj define a
function a by the Laurent series
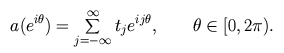
If the Toeplitz matrix T is banded,
then there exists some j0
such that tj=0 whenever
|j|>j0.
This implies that the function a is a
trigonometric polynomial.
The text of Böttcher and Silbermann [BS99]
provides a comprehensive introduction to the subject.
Widom's survey article [Wid65] is another good starting point.
We use the notation TN to denote the
N-by-N finite section of the infinite dimensional
Toeplitz matrix T.
The eigenvalues of finite banded Toeplitz matrices lie on curves in the
complex plane that have been characterized by Schmidt and Spitzer [SS60].
In contrast, the spectrum of the corresponding infinite dimensional Toeplitz
operator is the set of points in the complex plane that a(T)
encloses with non-zero winding number; see Theorem 1.17 of
[BS99].
The limit of the spectrum of banded Toeplitz matrices as the dimension goes
to infinity is thus typically very different from the spectrum of the limit.
This uncomfortable situation can be resolved by considering the behavior
of pseudospectra. Though the eigenvalues of the finite Toeplitz matrices
may fall on curves in the complex plane,
Landau [Lan75],
Reichel and Trefethen [RT92b], and
Böttcher [Böt94]
have observed that the resolvent norm
||(zI-TN)-1||
grows exponentially in the matrix dimension for all
z in the interior of the spectrum of the corresponding
infinite dimensional operator.
(As a result, it is difficult to accurately compute eigenvalues of
non-symmetric banded Toeplitz matrices even for matrices of relatively
modest dimensions, and this signals a warning against basing analysis
of finite Toeplitz matrices based on eigenvalues alone.)
Furthermore the above cited authors also concluded that the pseudospectra
of TN converge to the pseudospectra of T.
We now turn to several examples of computed pseudospectra of finite
Toeplitz matrices. A common theme to all these calculations is
the distance between the pseudospectral boundary and the eigenvalues
even for small values of epsilon.
Our first example is the simplest non-symmetric Toeplitz matrix,
the shift operator a(t)=t.
The infinite dimensional version is a classic example in
operator theory, and finite shift operators arise in
linear algebra in the Jordan cannonical form.
This matrix was the first example in the early survey
[Tre92].
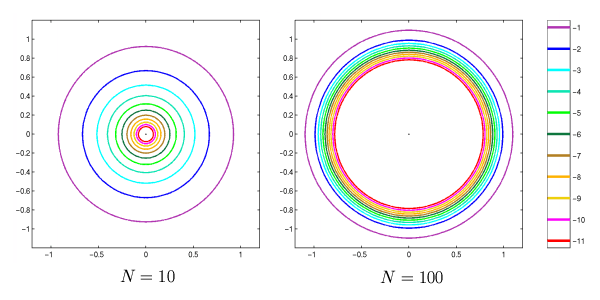
|
Figure 1. Spectrum and epsilon-pseudospectra
for the shift matrix of dimension 10 (left)
and dimension 100 (right).
Note the high degree of non-normality
present in the small matrix, and
how this non-normality explodes as the dimension is increased.
|
The "Grcar matrix" is another famous example.
Like the last example, it appears in the survey
[Tre92]
and has become a popular test problem in papers
on the computation of pseudospectra.
The matrix is determined by the symbol
|
Figure 2. Grcar matrix of dimension N=100.
The map of the symbol, a(T) (left) and the
spectrum and epsilon-pseudospectra (right).
|
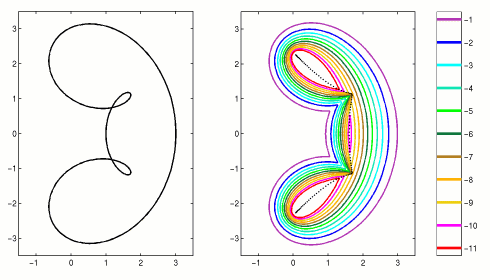
The pseudospectra of our next example resemble petals of a flower,
as seen in Figure 3. The corresponding symbol is
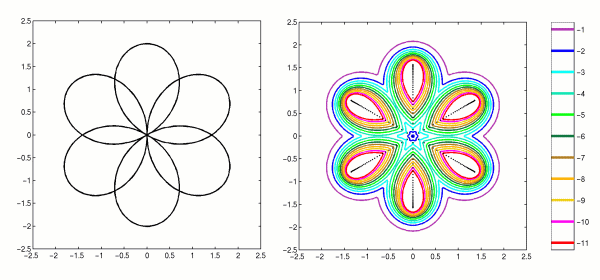
|
Figure 3. "Daisy" matrix of dimension N=200.
The map of the symbol, a(T) (left) and the
spectrum and epsilon-pseudospectra (right).
|
Our final example, in Figure 4, is from a banded Toeplitz matrix with a hole
in the spectrum of the corresponding infinite dimensional
operator. Notice that the pseudospectra do not grow
rapidly in the interior region where the winding number of
a(T) is zero.
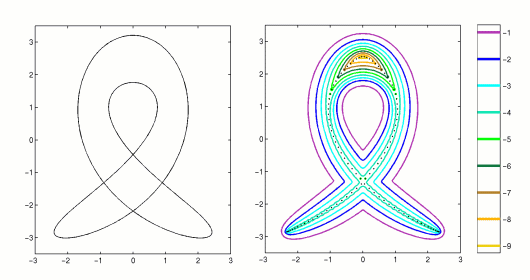
|
Figure 4. Truncation of a Toeplitz operator with a hole in the spectrum.
The map of the symbol, a(T) (left) and the
spectrum and epsilon-pseudospectra for a matrix of dimension N=100(right).
|
Supplemental Bibliography
References to works included in the
Pseudospectra Bibliography
are presented as links above, and are not repeated here.
| [SS60] |
P. Schmidt and F. Spitzer
The Toeplitz matrices of an arbitrary Laurent polynomial
Math. Scand. 8 (1960), 15--38.
MR 23 #A1977
|
| [Wid65] |
H. Widom
Toeplitz matrices
In Studies in Real and Complex Analysis,
Studies in Mathematics, vol. 3.
I. I. Hirschman, Jr., ed. Mathematical Association of America, Buffalo, N.Y., 1965.
|
|