Finding the shortest route

This page contains notes and slides from a talk I have given at Open Days in the Department of Computer Science.

In this talk, I will try to give you a rough idea of what Computer Science at university level is about.

I want to do that by discussing a programming problem with you: the problem is, given two towns, to find the shortest driving route from one to the other along the roads of Great Britain. The programming problem is one that our first year students study in their practical classes. You can try out the program in another part of our web site.

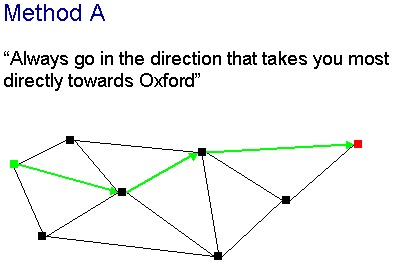There are various methods we might imagine using to solve this problem. The method I think I use when I'm sitting in the passenger seat of the car is this: choose a road that's going in roughly the right direction, and set out that way. When you reach a junction, choose the road that is going most directly towards your destination.

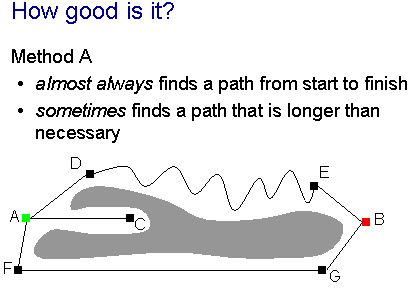Used with some common sense, this method works pretty well. But that's just the point: the method needs a bit of common sense, and common sense is exactly what computers don't have.

The picture here shows the roads around a lake. There's a peninsular C jutting out into the lake near town A, and if we used our method to find the best way from A to B, then we'd begin by going from A to C – and then we'd be stuck! Even without the peninsular, our method would take us from A to D, then along the winding mountain road to E, when a much better route is to go first to F (even going a bit further from the destination), then take the autoroute to G and on to B.

So method A won't be a very good basis for our program.

This is one of the first lessons of computer programming: that we need to find methods of solving problems that are always guaranteed to work, even if they are followed without any common sense. Methods that don't always give the correct answer, or do so only when used with a bit of intelligence, are useless – not because they never give the right answer, but because they can't be relied upon to do so in a crisis.

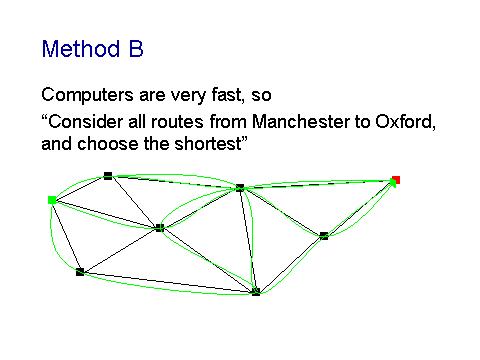Here's another method: since there are only finitely many ways of going from A to B, and since computers are very fast nowadays, why not get the computer to list all the ways of getting from A to B, and then pick the shortest?

This method will certainly always give the right answer. But it can be very slow on large road networks, because some networks contain huge numbers of possible routes.

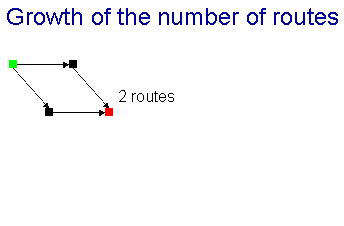For example, in this network, there are 2 routes from the green square to the red square.

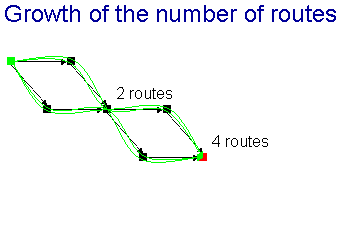In this network, there are 4 routes from the green square to the red square: we can go High and then High again, or High and then Low, or Low then High, or Low then Low.

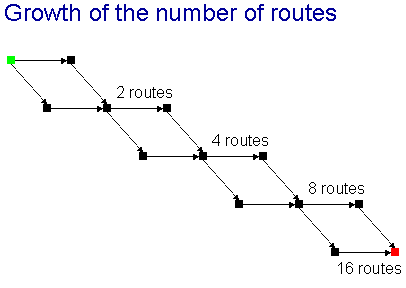If we add another diamond, then 4 becomes 8. And another diamond makes it 16 routes: the number doubles each time we add three more towns.

In the network we just looked at, the number of routes is roughly proportional to 2 to the power of n/3, where n is the number of towns. There are two ways to look at this, both equally discouraging:

• if we add three more towns, that will double the time needed to find the best route.
• if we get a computer that is twice as fast, we will not be able to use a database of towns that is much bigger at all: every time the speed of the computer doubles, we can add only three more towns to the map if we want the time to find the best route to stay the same.

So method B is also completely impractical.

A better method

What we need is a more systematic method – an algorithm, to use the Computer Science word. Such a method has been found for this problem: it consists of working out the best route to each town systematically, starting with towns near Manchester, and working outwards towards towns that are further away. We continue working outwards until we find the town we want to drive to by car.

In a little more detail, the towns on the map are divided into three sets:

• the white towns, for which the best route from Manchester has already been found.
• the grey towns, which are adjacent to one or more white towns. For these, we can estimate the best distance from Manchester as the distance of an adjacent white town + the length of the connection.
• the black towns, which we do not yet know how to reach at all.

The correct functioning of the algorithm depends on the fact (which can be proved mathematically) that the smallest distance estimate for any grey town does in fact give the true distance to that town.

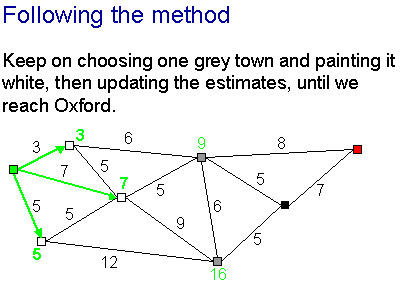If we want to go from Manchester to Oxford, the method is to begin with just Manchester coloured white, and colour other towns white one by one. The picture shows the state of play when the method has run for a short while and the three closest towns to Manchester are also coloured white.

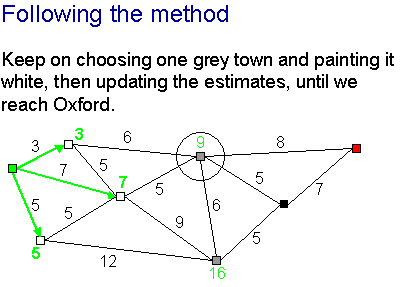At each stage, we choose the grey town with the smallest distance estimate ...

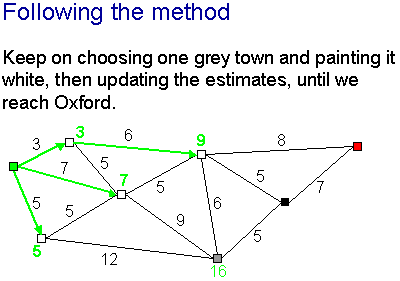... and colour it white ...

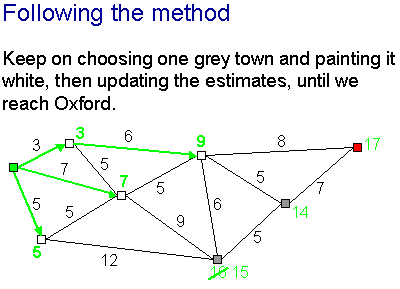... then update the distance estimates for all the towns adjacent to it. In the process, some black towns may become grey.

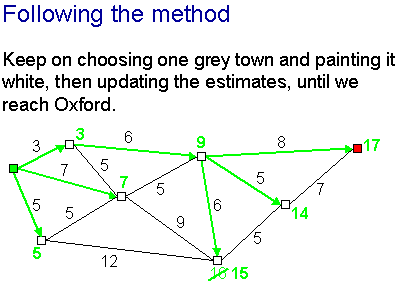We carry on like this until our desired destination is coloured white, and then we have found an accurate shortest distance to it.

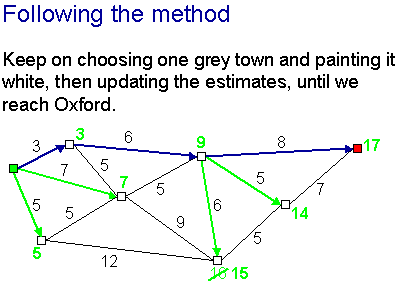If we want to know the route as well as the distance, we keep track of the route to each white town that is chosen as we go along, as shown by the blue arrows here.

This method always gives the right answer, and it does so in a reasonable time that is predictable from the number of towns in the map. The best thing of all would be if the time was proportional to the number n of towns. This isn't quite true, and the time is actually proportional to n log n if the program is implemented carefully. But this is good enough for practical purposes, because log n grows only slowly as n increases.

Once we understand how to solve the problem, we can implement the solution in any one of a number of programming languages. Here I've written programs in both Java, this year's most fashionable programming language, and Oberon Pascal, a language we use in teaching our students about programming. The reason for choosing Oberon is that it is really simple, and lets us concentrate on the important ideas behind the programs.

There are literally thousands of programming languages, and they are subject to fashions that come and go. That's why in university computer science (especially at Oxford) we emphasize reasoning about programs in a way that's independent of the programming language, and particularly the use of mathematics to construct rigorous arguments showing that programs work correctly. These things will retain their importance even when the fashion in programming languages changes.

The point is that once you really understand programming, the task of learning a new language is an easy one. If you know how to think about programs in the right way, you can learn C or Java in an afternoon. I know, because my students do it every year. When they answer those job adverts, they can say "I learnt Java in an afternoon: why did it take those other people a whole year?"