Greatest common divisors
 In this talk, I will try to give you a rough idea of what Computer
Science at university level is about.
In this talk, I will try to give you a rough idea of what Computer
Science at university level is about.
I want to do that by discussing a tiny programming problem with you. The problem is to compute the greatest common divisor of two integers. For example, suppose I have a floor that measures 259 by 111 centimetres, and I want to tile it with square tiles that I cut to a size that is a whole number of centimetres. What is the largest size of tile I could use?
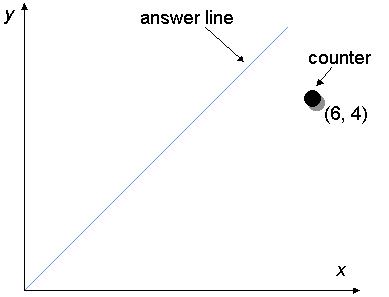 Here is a method for computing greatest common divisors that always works.
It does not use a computer, but instead it uses a piece of squared paper and a
counter. The paper is ruled with x and y axes and an "answer
line" that has equation x = y.
Here is a method for computing greatest common divisors that always works.
It does not use a computer, but instead it uses a piece of squared paper and a
counter. The paper is ruled with x and y axes and an "answer
line" that has equation x = y.
Initially we place the counter at a position (x, y) that has as its co-ordinates the two numbers for which we want to find the greatest common divisor: in this case 6 and 4.
If the initial position of the counter is not on the answer line (in this case, it isn't), then we perform a "move" as follows:
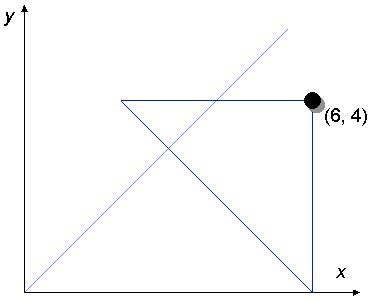 We find a right-angled isosceles triangle that has its right angle at the
position of the counter and one of its 45 degree angles on an axis. There will
be exactly one triangle that satisfies this description.
We find a right-angled isosceles triangle that has its right angle at the
position of the counter and one of its 45 degree angles on an axis. There will
be exactly one triangle that satisfies this description.
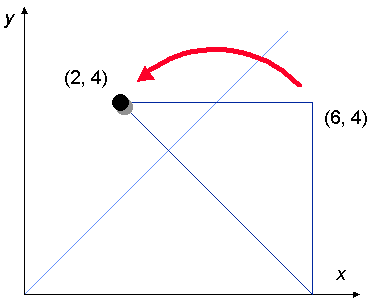 Next, we move the counter from the right angle to the other 45 degree
angle (the one that is not on an axis). In the example, we move the counter
from (6, 4) to (2, 4).
Next, we move the counter from the right angle to the other 45 degree
angle (the one that is not on an axis). In the example, we move the counter
from (6, 4) to (2, 4).
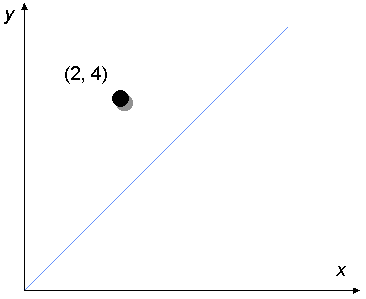 This completes the move.
This completes the move.
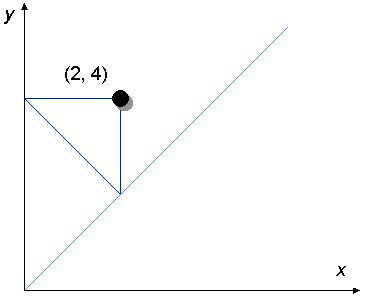 If the counter is still not on the answer line (it isn't), we carry out
another move.
If the counter is still not on the answer line (it isn't), we carry out
another move.
Again, we construct a right-angled isosceles triangle that has its right angle under the counter and one of its 45 degree angles on an axis (this time, it's the y axis).
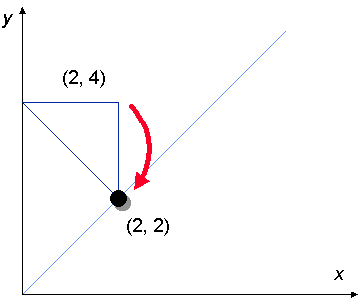 Then we move the counter to the other 45 degree angle. In the example, we
move the counter from (2, 4) to (2, 2).
Then we move the counter to the other 45 degree angle. In the example, we
move the counter from (2, 4) to (2, 2).
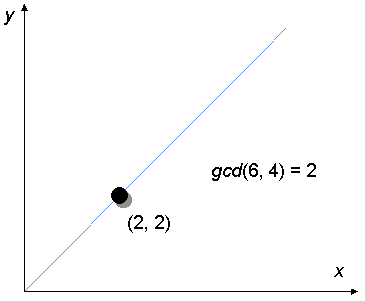 We continue making moves like this until the counter ends up on the answer
line, with equation x = y. In the example, we have reached the
answer line after two moves. The x and y co-ordinates of the
counter are the same, and we may take either of them as the greatest common
divisor of our original pair of numbers.
We continue making moves like this until the counter ends up on the answer
line, with equation x = y. In the example, we have reached the
answer line after two moves. The x and y co-ordinates of the
counter are the same, and we may take either of them as the greatest common
divisor of our original pair of numbers.
In the example, we find that the greatest common divisor of 6 and 4 is 2. And that's correct!
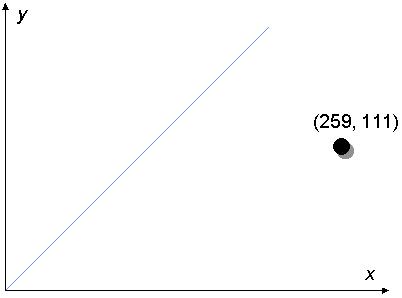 If we play the game with 259 and 111 instead of 6 and 4, it takes
four moves before we hit the answer line.
If we play the game with 259 and 111 instead of 6 and 4, it takes
four moves before we hit the answer line.
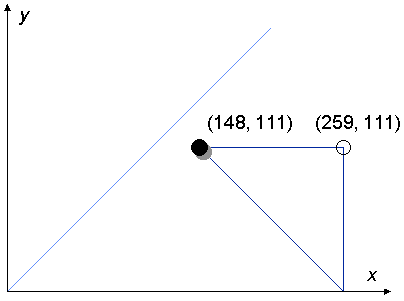 one . . .
one . . .
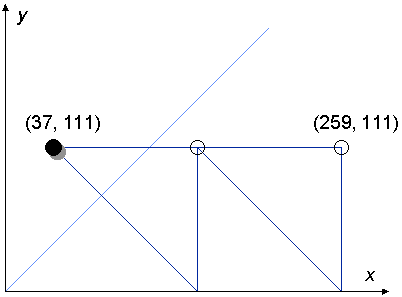 two . . .
two . . .
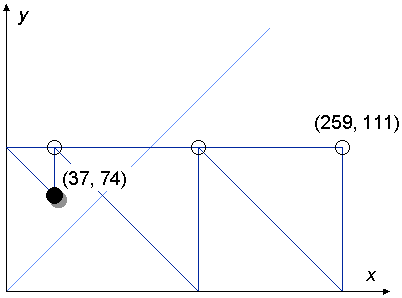 three . . .
three . . .
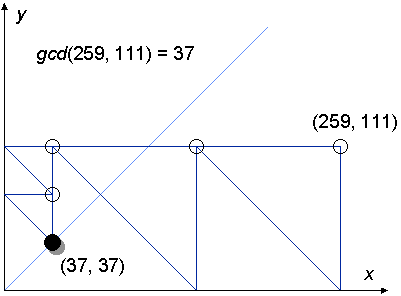 four.
four.
The final position of the counter is (37, 37), so we read off the greatest common divisor of 259 and 111 as 37.
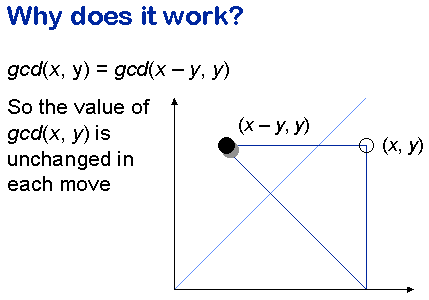 Why does this method work? The key is to analyse what happens
in each step. If the position of the counter before the step is
(x, y) and x is greater than y –
so that the counter is below the answer line, then the
new position of the counter is (x - y, y).
We can prove algebraically (though we won't go into it here) that
the greatest common divisor of x - y and y
is the same as the greatest common divisor of x and y.
So moving the counter from (x, y) to (x -
y, y) does not change the greatest common divisor
of its co-ordinates.
Why does this method work? The key is to analyse what happens
in each step. If the position of the counter before the step is
(x, y) and x is greater than y –
so that the counter is below the answer line, then the
new position of the counter is (x - y, y).
We can prove algebraically (though we won't go into it here) that
the greatest common divisor of x - y and y
is the same as the greatest common divisor of x and y.
So moving the counter from (x, y) to (x -
y, y) does not change the greatest common divisor
of its co-ordinates.
A similar argument works if the counter begins above the answer line.
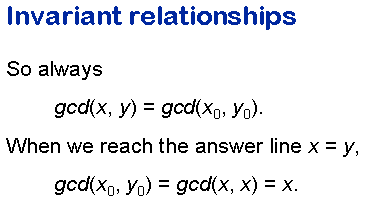 The greatest common divisor of the counter's co-ordinates does
not change when we execute a single move. It follows that however
many moves we execute, the greatest common divisor of the
counter's co-ordinates is equal to the greatest common divisor
of its original co-ordinates, which I've written here as x0
and y0.
The greatest common divisor of the counter's co-ordinates does
not change when we execute a single move. It follows that however
many moves we execute, the greatest common divisor of the
counter's co-ordinates is equal to the greatest common divisor
of its original co-ordinates, which I've written here as x0
and y0.
All being well, we eventually reach the answer line, where x = y, so both co-ordinates are the same. The greatest common divisor of x and the same number x is obvious: it is just x itself. So when we reach the answer line, we can read off the greatest common divisor of the counter's co-ordinates, and this is equal to the greatest common divisor of the counter's original co-ordinates.
 Of course, if we wanted to compute the greatest common divisor
of big numbers, we wouldn't really use a piece of squared paper
and a counter. We'd use a computer instead, and make the computer
simulate the actions of playing our little game. To do that, we'd
have to express the rules of the game as a computer program.
Of course, if we wanted to compute the greatest common divisor
of big numbers, we wouldn't really use a piece of squared paper
and a counter. We'd use a computer instead, and make the computer
simulate the actions of playing our little game. To do that, we'd
have to express the rules of the game as a computer program.
Here are the rules expressed as a program in one of my favourite programming languages, Pascal. The first line of the program says that the rest of the program is to be obeyed repeatedly until the test x ≠ y is false – that is, until we reach the answer line. The rest of the program asks the computer to find out whether the counter is below the answer line (if x > y) or above it, and to move the counter either to the left (by changing the x co-ordinate) or downwards (by changing the y co-ordinate) as appropriate. So the program captures precisely the rules by which we have been playing the game.
 Exactly the same rules can be written as a program in other languages:
here they are written in one of my unfavourite programming languages,
BASIC.
Exactly the same rules can be written as a program in other languages:
here they are written in one of my unfavourite programming languages,
BASIC.
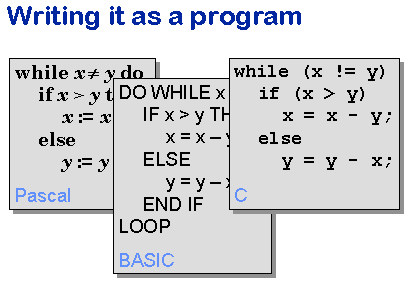 And here they are written in some other people's favourite programming
language, C.
And here they are written in some other people's favourite programming
language, C.
The point is that it doesn't matter which programming language we use to write down the rules of the game. The interesting thing is not what language we use, but the game itself, and most importantly the reasons why it works. These things are the same whatever language we use.
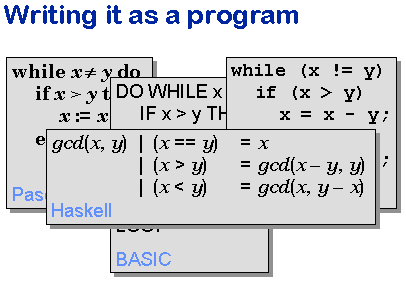 As it happens, we use a special language in our first year
programming that is a little different in flavour from Pascal or BASIC
or C. It's called Haskell, and we chose it because it makes the link
between programming and mathematical reasoning especially direct. The
link is there in other programming languages, but Haskell makes it
especially easy to work with.
As it happens, we use a special language in our first year
programming that is a little different in flavour from Pascal or BASIC
or C. It's called Haskell, and we chose it because it makes the link
between programming and mathematical reasoning especially direct. The
link is there in other programming languages, but Haskell makes it
especially easy to work with.
Although Haskell is not a language that you'll find mentioned in job adverts, it is actually extremely powerful. Consequently, our first-year students are able to write programs (and explain why they work) that would stump third-year students using a conventional language. We also use a modern dialect of Pascal called Oberon, again because it is a simple language that reveals the true principles of programming.
There are literally thousands of programming languages, and they
are subject to fashions that come and go.
That's why in university computer science (especially at Oxford) we emphasize reasoning about programs in a way that's independent of the programming language. We particularly emphasize the use of mathematics to construct rigorous arguments showing that programs work correctly. These things will retain their importance even when the fashion in programming languages changes.
The point is that once you really understand programming, the task of learning a new language is an easy one. If you know how to think about programs in the right way, you can learn C in an afternoon. I know, because my students do it every year. When they answer those job adverts, they can say "I learnt C in an afternoon: why did it take those other people a whole year?"
