Fast N-body computation
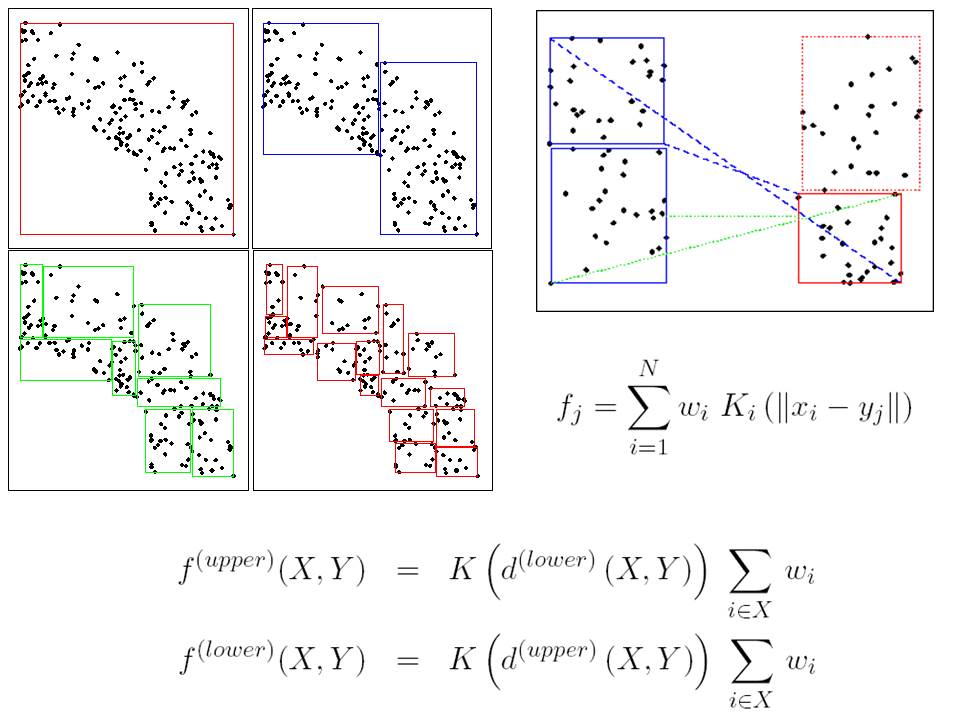
Many algorithms for statistical inference have a O(N2) time dependence on the size of the state space (N). For example, at the heart of the belief propagation algorithm is an expensive operation called message passing. The cost of this operation is O(nN2), where n is the number of nodes in the probabilistic graphical model and N is the number of discrete values the node (random variable) takes. The N2 component of the cost is particularly large when we discretize a continuous state space using deterministic or Monte Carlo grids.
The N2 cost arises whenever one computes a kernel density estimate. In addition to message passing, many other machine learning algorithms are subject to this expensive operation. The list includes Gaussian processes, radial basis networks, SVMs, particle smoothing, population Monte Carlo methods, multidimensional scaling and kernel methods for dimensionality reduction, classification, regression, approximate nearest neighbour matching, and semi-supervised learning. This cost also arises when one is interested in the max operator (as in max belief propagation) and nearest neighbour search.
In recent years, researchers in different communities (physics, numerical computation, machine learning and computer vision) have put forward algorithms to reduce this cost to O(NlogN) and even O(N) in some cases. Examples of these techniques include fast multipole methods, the fast Gauss transform, distance transforms, kd-trees, ball trees, dual tree recursions and several other more specialized techniques.
Our software for kd-tress and the fast Gauss transform is freely available.
These introductory slides provide an overview of the methodology.
Selected Publications
-
Empirical Testing of Fast Kernel Density Estimation Algorithms
Dustin Lang‚ Mike Klaas and Nando de Freitas
No. UBC TR−2005−03. University of British Columbia‚ Department of Computer Science. 2005.
Details about Empirical Testing of Fast Kernel Density Estimation Algorithms | BibTeX data for Empirical Testing of Fast Kernel Density Estimation Algorithms | Download (pdf) of Empirical Testing of Fast Kernel Density Estimation Algorithms
-
Fast particle smoothing: if I had a million particles
Mike Klaas‚ Mark Briers‚ Nando de Freitas‚ Arnaud Doucet‚ Simon Maskell and Dustin Lang
In International Conference on Machine Learning (ICML). Pages 481–488. New York‚ NY‚ USA. 2006. ACM.
Details about Fast particle smoothing: if I had a million particles | BibTeX data for Fast particle smoothing: if I had a million particles | DOI (10.1145/1143844.1143905) | Link to Fast particle smoothing: if I had a million particles
-
Fast maximum a posteriori inference in Monte Carlo state spaces
Mike Klaas‚ Dustin Lang and Nando de Freitas
In Artificial Intelligence and Statistics (AISTATS). 2005.
Details about Fast maximum a posteriori inference in Monte Carlo state spaces | BibTeX data for Fast maximum a posteriori inference in Monte Carlo state spaces | Download (pdf) of Fast maximum a posteriori inference in Monte Carlo state spaces
