Categorical Tensor Network States
Stephen R.Clark Jacob D. Biamonte and Dieter Jaksch
Abstract
We examine the use of the mathematics of category theory in the description
of quantum states by tensor networks. This approach enables the development of
a categorical framework allowing a solution to the quantum decomposition
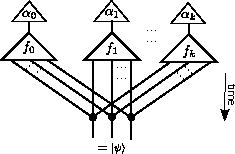
problem. Specifically, given an n-body quantum state ψ, we present
a general method to factor ψ into a tensor network. Moreover, this
decomposition of ψ uses building blocks defined mathematically in
terms of purely diagrammatic laws. We use the solution to expose a previously
unknown and large class of quantum states which we prove can be sampled
efficiently and exactly. This general framework of categorical tensor network
states, where a combination of generic and algebraically defined tensors
appear, enhances the theory of tensor network states.
Blogs about this paper:
(i) http://golem.ph.utexas.edu/category/2010/09/bimonoids_from_biproducts.html
(ii) http://johncarlosbaez.wordpress.com/2010/09/29/jacob-biamonte-on-tensor-networks/
Talks about this paper:
(i) http://new.iqc.ca/news-events/calendar/generated/jacob-biamonte-2010-12-2 (IQC, Institute for Quantum Computing
University of Waterloo, Canada)
Link to arXiv version:
* http://arxiv.org/abs/1012.0531