Quantum Group

We are a group focused on quantum computation and the foundations of quantum theory. The group is led by Professor Jonathan Barrett and Professor Aleks Kissinger.

Some of the research areas we are most intersted in are:

• Quantum software, compilers, and optimisation
• Causality in quantum theory and indefinite causal structures
• Diagrammatic reasoning and the ZX-calculus
• Generalised/operational probabilistic theories

Also connected to the group is Dr Stefano Gogioso and visiting professor/fellows Professor Bob Coecke (chief scientist at Quantinuum), Professor Samson Abramsky (professor at UCL), and Professor Giulio Chiribella (professor at HKU).

Click here to access the extensive Oxford Quantum Talk Archive, our video archive of research talks.

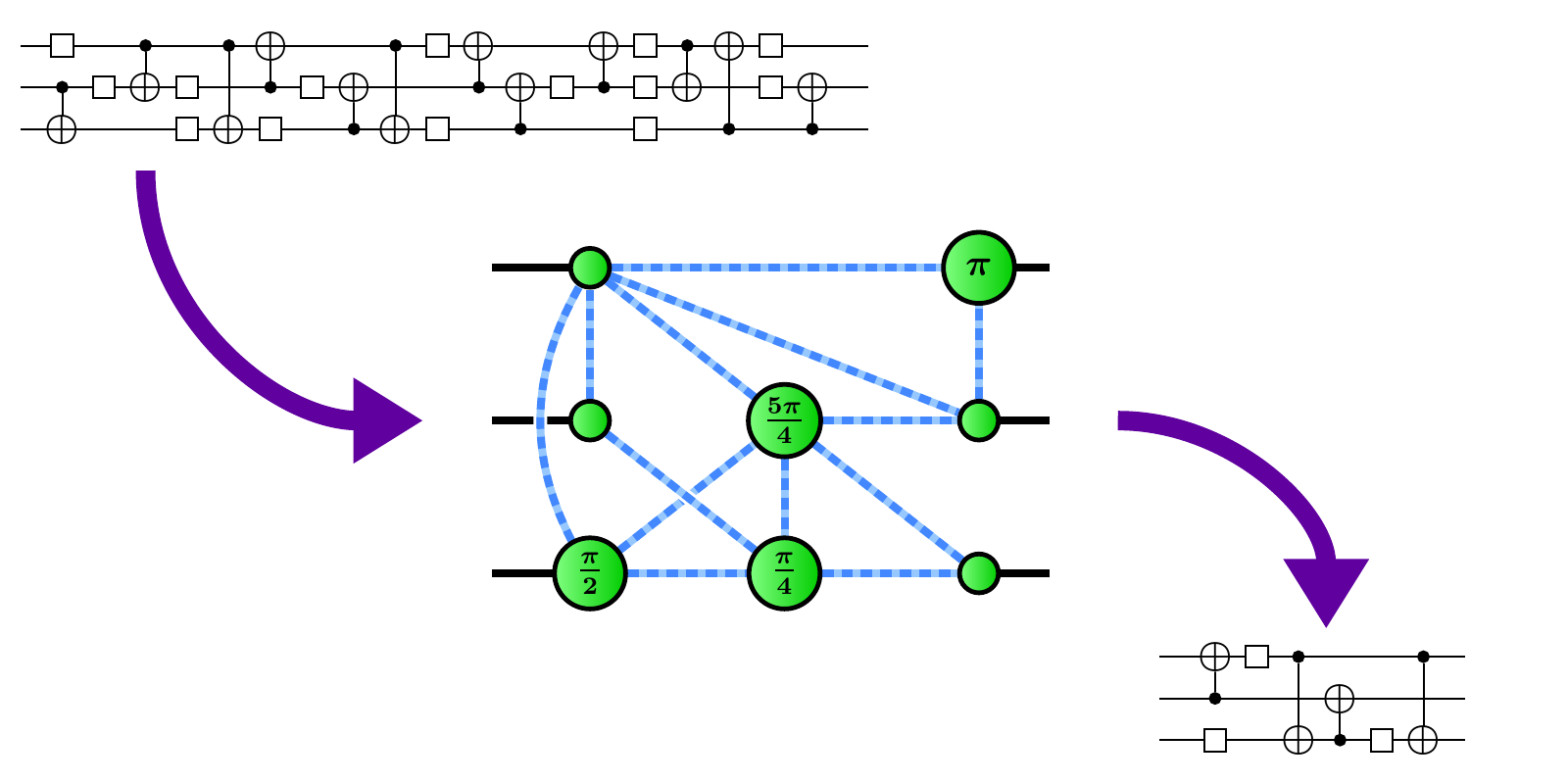
Quantum software, compilers, and the ZX-calculus

Quantum computers can, in principle, solve computational problems that are far out of reach even for todays most powerful supercomputers. Quantum software refers to the code that runs on those computers. Of central importance in this area is the development of new quantum algorithms to take advantage of these drastically different computational platforms. However, like in classical software development, the field of quantum software is much broader than just the design of new algorithms.

A central research theme in our group is quantum compilation. This is a relatively new field that studies a whole host of theoretical and practical problems involved in translating the high-level description of a quantum algorithm into something that is runnable a quantum hardware.

Examples of such problems are the design of new quantum programming languages, which allow developers to write quantum algorithms in ways that abstract away from distracting details and think about computations in ways that are more fundamentally quantum.

Another example is quantum circuit synthesis and optimisation. Quantum circuits form a de facto "assembly language" for quantum computers, describing computations as sequences of basic physical operations, called gates, which can be implemented on hardware. Gates take time and introduce noise into a computation, hence reducing the number or depth of gates in a circuit can drastically increase the capabilities of todays (very limited) quantum computers.

In addition to abstract optimisation of quantum circuits, there is much to be gained from hardware-aware compilation techniques, which take the specific capabilities and constraints of a hardware platform into account. Ion trap quantum computers have very different characteristics from superconducting ones, and quantum computations based on optics are best described in ways that are totally different from circuits. Hence, one can design compilers that do things like circuit routing to account for connectivity constraints in quantum memories, take advantage of native and global gates available on certain hardware platforms, and translate to/from measurement-based quantum computations (MBQC) which are more well-suited to optical hardware.

Much of this work uses the ZX-calculus, a graph-based "swiss army knife" for reasoning about quantum computations. This theoretical tool was originally developed at Oxford, and now forms the basis of quantum compilation software like PyZX and is being increasingly used in quantum software research teams in industry.

If you are new to this stuff, here's a couple of good places to start:

• ZX-calculus for the working quantum computer scientist - an accessible tutorial for anyone with some quantum computing/circuits background
• Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning - a.k.a. "the Dodo book", a complete into to quantum info, computing, and foundations using the mathematics of diagrams

Here are some recent papers:

• Phase-free ZX diagrams are CSS codes (...or how to graphically grok the surface code)
• Graph-theoretic Simplification of Quantum Circuits with the ZX-calculus
• CNOT circuit extraction for topologically-constrained quantum memories
• Classical simulation of quantum circuits with partial and graphical stabiliser decompositions
• Qutrit metaplectic gates are a subset of Clifford+T
• Quantum double aspects of surface code models

We also maintain some open source software projects.

Quantum foundations and quantum causal structure

Causality is a fundamental concept, both in fundamental physics and our everyday lives. In relativity theory, the causality principle states that information propagates through spacetime at a finite rate (namely, the speed of light). This limitation is what enables us to unambiguously say when events have happened "before" or "after" others and avoid logical paradoxes, even in a universe where time is a relative concept.

On the other hand, in statistical modelling, causality means something quite different. While relativistic causality puts constraints on which events can in principle affect one another, causality in statistics measures how much a single event A does influence another event B. Our work studies the point where these two notions of causality meet, and particularly what happens when quantum processes enter the mix.

While classical functional or statistical causal models are by now well-established, they run in to limitations when trying to make sense situations involving quantum nonlocality. Classical causal models couched in the traditional formulation of Reichenbach's common cause principle don't seem to work any more, as quantum theory predicts correlations between distant events that are simply too strong to be explained by any local, classical common cause. Should we abandon this principle, or should we update it to account for the quantum world? In either case, what should the resulting quantum causal models look like?

In an even more drastic departure from classical notions of causality, recent theoretical work and experiments have suggested the possibility of indefinite causal structures. These are scenarios involving multiple events or agents which cannot be explained by assuming any fixed causal order. Such scenarios can be realised modestly by particles traversing an apparatus in superpositions of paths and might even be possible to realise making use of superpositions of spacetimes as predicted by a quantum theory of gravity.

In the quantum group, our focus is on developing quantum causal models and studying their properties. Along the way, we have developed mathematical and logical tools for studying definite and indefinite causal structures, and reasoning about causal relationships, consistency, and paradox in these frameworks.

We are part of an international consortium on the Quantum Information Structure of Spacetime, which unites experts in quantum information, quantum foundations, and quantum gravity to answer fundamental questions about space, time, and causal structure in the quantum regime.

Here is a selection of some recent papers from the group:

• Quantum Causal Models
• Device-independent certification of indefinite causal order in the quantum switch
• Cyclic Quantum Causal Models
• Causal and compositional structure of unitary transformations
• Causal Inference by String Diagram Surgery
• Higher-order causal theories are models of BV-logic
• The computational landscape of general physical theories

Joining the group

If you'd like more information about joining the group, as a postdoctoral researcher or as a DPhil student, please contact Professor Jonathan Barrett and Professor Aleks Kissinger. We have supported postdoctoral fellowship applications for strong applicants. The Engineering and Physical Sciences Research Council and the Royal Society have annual postdoctoral fellowship competitions, some of which are open to non-British nationals. The department also awards DPhil scholarships each year to the strongest UK and overseas applicants.

If you're already doing a Masters degree in Oxford and might be interested in doing your project with a member of our group, please get in touch as soon as possible with one of the group members listed above.

If you're an undergraduate and would like to learn more about the sorts of things we work on, have a look at the MSc in Mathematics and the Foundations of Computer Science.

Mailing lists

We run an international quantum foundations mailing list. To subscribe, send a blank email to quantum-foundations-subscribe@maillist.ox.ac.uk. We also have a separate list to announce local events related to our group's activities; to subscribe, send a blank email to quantum-announcements-join@cs.ox.ac.uk.

Funding

We gratefully acknowledge support from the Airforce Office of Scientific Research and the John Templeton Foundation.

Selected Publications

View All

• External traced monoidal categories

  Nick Hu

  Master's Thesis 2019.

  Details about External traced monoidal categories | BibTeX data for External traced monoidal categories | Download  (pdf) of External traced monoidal categories

• Contextuality and noncommutative geometry in quantum mechanics

  Nadish de Silva and Rui Soares Barbosa

  In Communications in Mathematical Physics. Vol. 365. No. 2. Pages 375–429. 2019.

  Earlier partial version (“Partial and total ideals of von Neumann algebras”) available as arXiv:1408.1172 [math.OA]

  Details about Contextuality and noncommutative geometry in quantum mechanics | BibTeX data for Contextuality and noncommutative geometry in quantum mechanics | DOI (10.1007/s00220-018-3222-9)

• Minimum quantum resources for strong non−locality

  Samson Abramsky‚ Rui Soares Barbosa‚ Giovanni Carù‚ Nadish de Silva‚ Kohei Kishida and Shane Mansfield

  In Mark M. Wilde, editor, Proceedings of 12th Conference on the Theory of Quantum Computation‚ Communication and Cryptography (TQC 2017). Vol. 73 of Leibniz International Proceedings in Informatics (LIPIcs). Pages 9:1–9:20. Dagstuhl‚ Germany. 2018. Schloss Dagstuhl–Leibniz−Zentrum fuer Informatik.

  Accepted for communication at 14th International Conference on Quantum Physics and Logic (QPL 2017); E−print: arXiv:1705.09312 [quant−ph]

  Details about Minimum quantum resources for strong non−locality | BibTeX data for Minimum quantum resources for strong non−locality | DOI (10.4230/LIPIcs.TQC.2017.9) | Link to Minimum quantum resources for strong non−locality